4 Verteilungen
In diesem Abschnitt untersuchen wir Verteilungen einzelner Variablen. Histogramme und Balkendiagramme veranschaulichen die Häufigkeits- oder Wahrscheinlichkeitsverteilung, wie in den folgenden Abbildungen dargestellt. Verteilungen sind die Grundlage für Simulationen, z. B. in der Monte-Carlo-Methode, wie im Tutorial zur Fahrzeugausfallzeit gezeigt.
4.1 Diskrete Verteilungen
Diskrete Verteilungen beschreiben Zufallsvariablen mit abzählbaren Werten. Wir betrachten die Bernoulli-Verteilung, Binomial-Verteilung und Poisson-Verteilung, die häufig in der Statistik und realen Anwendungen vorkommen.
4.1.1 Bernoulli-Verteilung
Die Bernoulli-Verteilung modelliert eine Zufallsvariable mit genau zwei möglichen Ergebnissen, z. B. einen Münzwurf: „Kopf“ (\(X = 1\)) mit Wahrscheinlichkeit \(p\) oder „Zahl“ (\(X = 0\)) mit Wahrscheinlichkeit \(1-p\). Die Wahrscheinlichkeitsfunktion lautet:
\[P(X = x) = \begin{cases}
p & \text{für } x = 1, \\
1-p & \text{für } x = 0.
\end{cases}\]
Wir schreiben \(X \sim \text{Bernoulli}(p)\). Für eine faire Münze gilt \(p = 0.5\), also \(X \sim \text{Bernoulli}(0.5)\).
Figure 4.1 zeigt die Verteilung für eine faire Münze. Diese einfache Verteilung ist die Basis für komplexere Modelle wie die Binomial-Verteilung und findet Anwendung in Entscheidungen mit Ja/Nein-Ergebnissen.
import numpy as np
import matplotlib.pyplot as plt
p = 0.5
x = [0, 1] # Einfache Liste statt NumPy-Array für Klarheit
P_X = [1-p, p]
plt.bar(x, P_X, color='skyblue', width=0.6)
plt.xlabel('Ergebnis (0 = Zahl, 1 = Kopf)')
plt.ylabel('Wahrscheinlichkeit')
plt.title('Bernoulli-Verteilung ($p = 0.5$)')
plt.ylim(0, 1)
plt.xticks(x)
plt.grid(axis='y', alpha=0.3)
plt.show()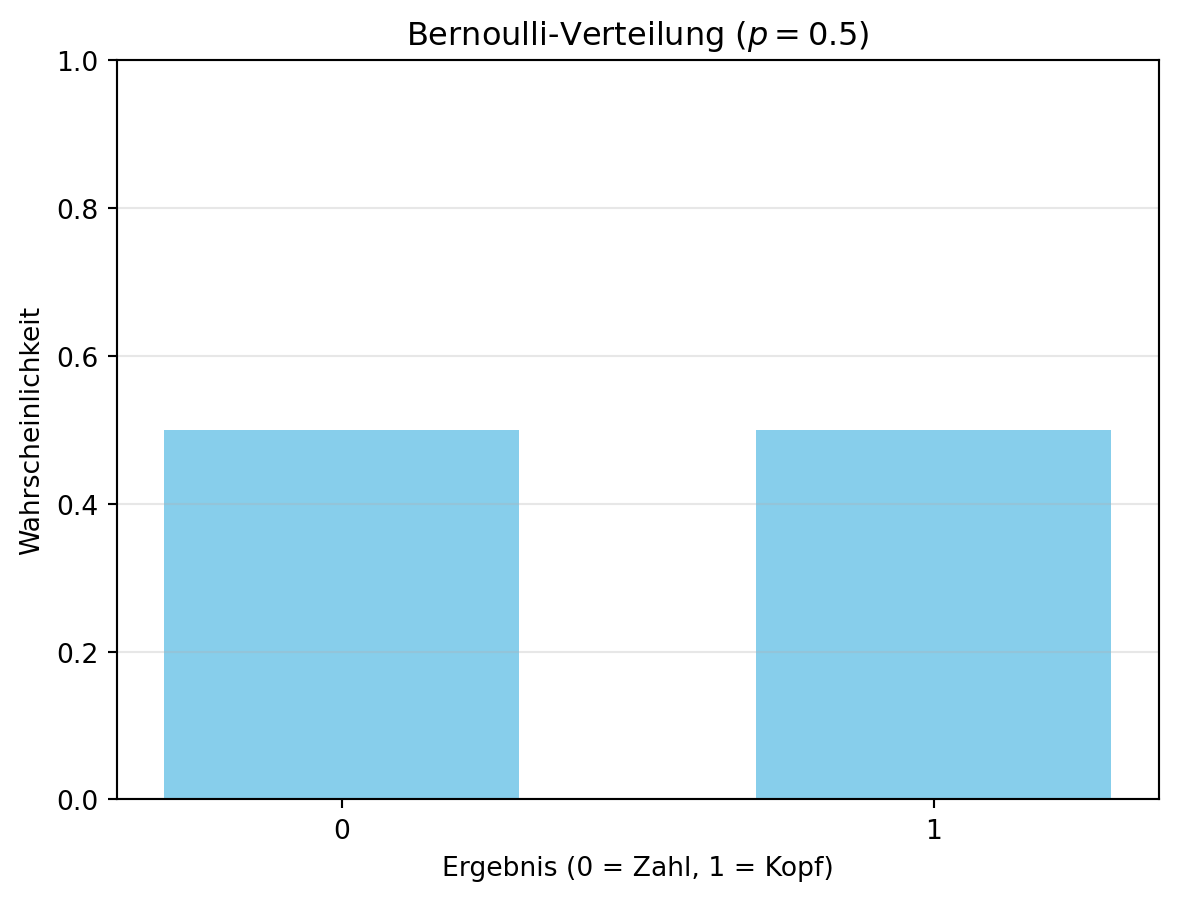
In Figure 4.1 wird jeder möglichen Realisierung der Zufallsvariablen \(X\) die theoretische Wahrscheinlichkeit zugeordnet. Im Gegensatz zu Histogrammen, die empirische Häufigkeiten darstellen, zeigt diese Abbildung die Wahrscheinlichkeitsverteilung direkt.
4.1.1.1 Erwartungswert und Varianz der Bernoulli-Verteilung
Der Erwartungswert \(E(X)\) einer Verteilung beschreibt ihre zentrale Tendenz – den durchschnittlichen Wert der Zufallsvariablen. Für eine diskrete Zufallsvariable \(X\) gilt:
\[E(X) = \sum_{x} x \cdot P(X = x).\]
Bei der Bernoulli-Verteilung (\(X \sim \text{Bernoulli}(p)\)) ist:
\[E(X) = 0 \cdot (1-p) + 1 \cdot p = p.\]
Für eine faire Münze (\(p = 0.5\)) ist \(E(X) = 0.5\).
Die Varianz \(\text{Var}(X)\) misst die Streuung der Verteilung – wie stark die Werte um den Erwartungswert schwanken. Sie wird berechnet als:
\[\text{Var}(X) = \sum_{x} (x - E(X))^2 \cdot P(X = x).\]
Für die Bernoulli-Verteilung ergibt sich:
\[\text{Var}(X) = (0 - p)^2 \cdot (1-p) + (1 - p)^2 \cdot p = p \cdot (1-p).\]
Bei \(p = 0.5\) ist \(\text{Var}(X) = 0.5 \cdot 0.5 = 0.25\).
4.1.2 Binomialverteilung
Stellen wir uns vor, wir wiederholen einen Münzwurf \(n\)-mal unabhängig mit der Wahrscheinlichkeit \(p\) für „Kopf“. Die Zufallsvariable \(Y\) zählt die Anzahl der Kopfwürfe und folgt einer Binomialverteilung: \(Y \sim \text{Bin}(n, p)\). Die Wahrscheinlichkeitsfunktion lautet:
\[P(Y = k) = \binom{n}{k} p^k (1-p)^{n-k},\]
wobei \(\binom{n}{k}\) die Anzahl der Möglichkeiten ist, \(k\) Erfolge in \(n\) Versuchen zu erzielen.
Figure 4.2 zeigt die Verteilung für \(n = 10\) und \(p = 0.5\). Die Binomialverteilung ist eine Erweiterung der Bernoulli-Verteilung und nützlich, um Häufigkeiten in wiederholten Experimenten zu modellieren.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom
n = 10
p = 0.5
y = np.arange(0, n + 1)
P_Y = binom.pmf(y, n, p)
plt.bar(y, P_Y, color='skyblue', width=0.8)
plt.xlabel('Anzahl der Kopfwürfe ($Y$)')
plt.ylabel('Wahrscheinlichkeit')
plt.title(f'Binomialverteilung ($n = {n}$, $p = {p}$)')
plt.xticks(y)
plt.grid(axis='y', alpha=0.3)
plt.show()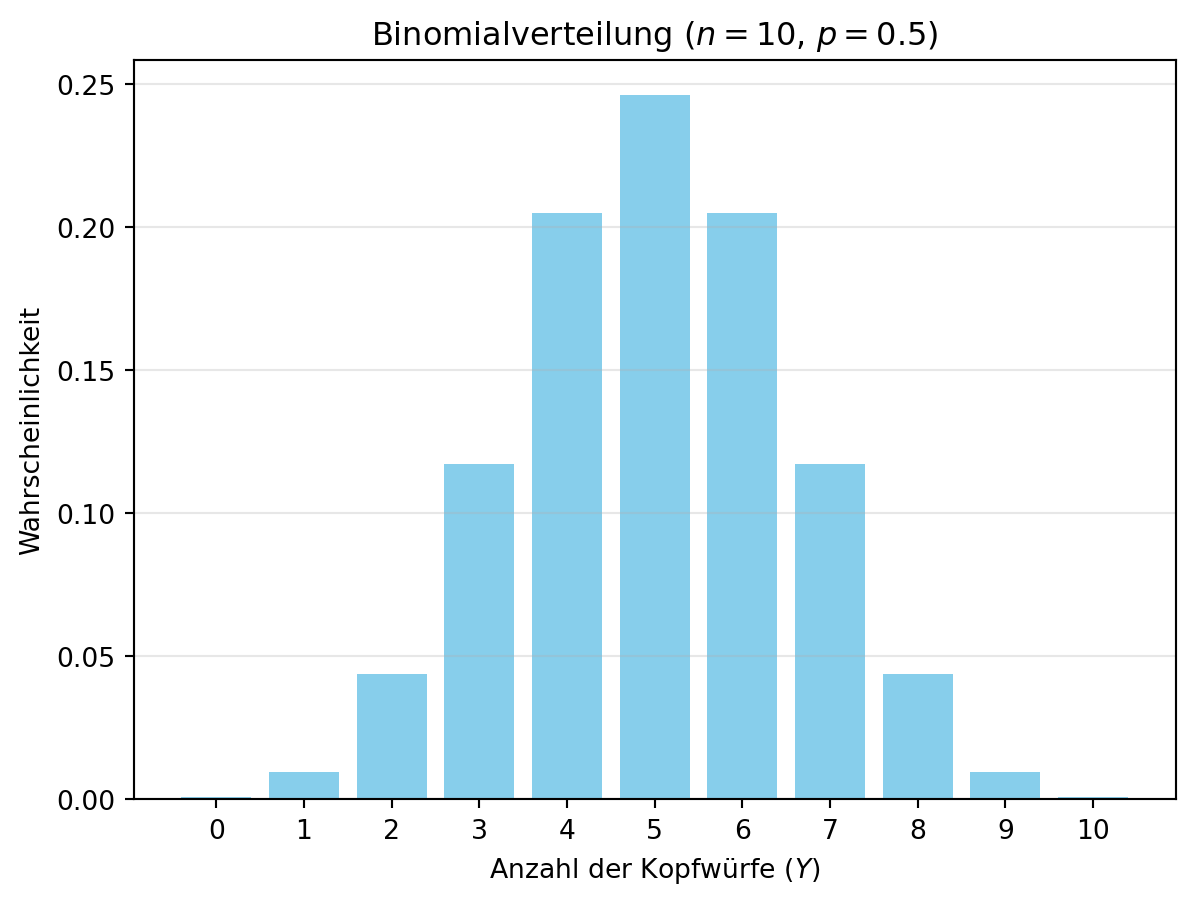
Stellen wir uns vor, wir wiederholen einen Münzwurf \(n\)-mal. Die Würfe sind unabhängig und identisch verteilt (i.i.d.), d. h., jeder Wurf hat die gleiche Wahrscheinlichkeit \(p\) für „Kopf“ und ist unbeeinflusst von den anderen. Die Zufallsvariable \(Y\) zählt die Anzahl der Kopfwürfe und folgt einer Binomialverteilung: \(Y \sim \text{Bin}(n, p)\). Die Wahrscheinlichkeitsfunktion ist:
\[P(Y = y) = \binom{n}{y} \cdot p^y \cdot (1-p)^{n-y},\]
wobei \(\binom{n}{y}\) der Binomialkoeffizient ist. Dieser gibt an, auf wie viele Arten \(y\) Erfolge in \(n\) Versuchen auftreten können und wird definiert als:
\[\binom{n}{y} = \frac{n!}{y! \cdot (n - y)!}.\]
4.1.2.1 Beispiel: Münzwurf
Für \(n = 10\) Würfe mit einer fairen Münze (\(p = 0.5\)) ist \(Y \sim \text{Bin}(10, 0.5)\). Dies wurde in Figure 4.2 gezeigt.
4.1.2.2 Beispiel: Gewinnlose
Passen wir die Werte an: Beim Ziehen von 10 Losen, wobei die Wahrscheinlichkeit für ein Gewinnlos \(p = 0.1\) beträgt, gilt \(Y \sim \text{Bin}(10, 0.1)\). Die Zufallsvariable \(Y\) zählt die Anzahl der Gewinnlose. Figure 4.3 zeigt diese Verteilung. Solche Modelle sind nützlich, um Erfolge in wiederholten, unabhängigen Versuchen zu analysieren – ähnlich wie im Tutorial zur Fahrzeugausfallzeit, wo Verteilungen für Komponenten genutzt werden.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom
n = 10
p = 0.1
y = np.arange(0, n + 1)
P_Y = binom.pmf(y, n, p)
plt.bar(y, P_Y, color='skyblue', width=0.8)
plt.xlabel('Anzahl der Gewinnlose ($Y$)')
plt.ylabel('Wahrscheinlichkeit')
plt.title(f'Binomialverteilung ($n = {n}$, $p = {p}$)')
plt.xticks(y)
plt.grid(axis='y', alpha=0.3)
plt.show()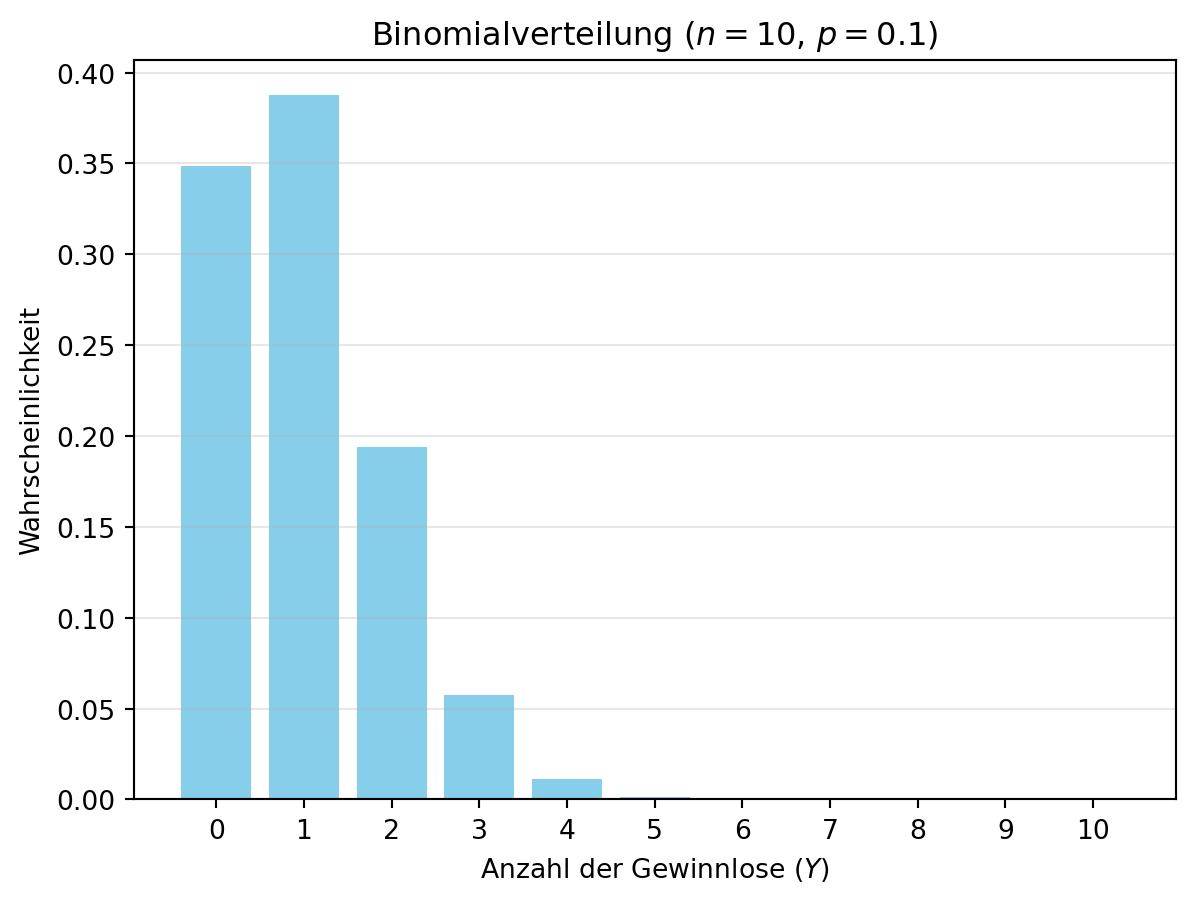
4.1.2.3 Erwartungswert und Varianz der Binomialverteilung
Der Erwartungswert \(E(Y)\) der Binomialverteilung (\(Y \sim \text{Bin}(n, p)\)) gibt die erwartete Anzahl der Erfolge in \(n\) Versuchen an:
\[E(Y) = n \cdot p.\]
Für \(n = 10\) und \(p = 0.1\) (Gewinnlose) ist \(E(Y) = 10 \cdot 0.1 = 1\).
Die Varianz \(\text{Var}(Y)\) misst die Streuung um diesen Erwartungswert:
\[\text{Var}(Y) = n \cdot p \cdot (1-p).\]
Im Beispiel ist \(\text{Var}(Y) = 10 \cdot 0.1 \cdot 0.9 = 0.9\). Diese Werte helfen, die Verteilung zu charakterisieren, z. B. in Simulationen wie im Tutorial.
4.1.3 Diskrete Gleichverteilung
Die diskrete Gleichverteilung (auch Uniformverteilung) beschreibt eine Zufallsvariable, bei der alle möglichen Werte innerhalb eines Intervalls die gleiche Wahrscheinlichkeit haben. Im Gegensatz zum Würfelbeispiel, wo die Werte bei 1 beginnen, kann das Intervall beliebig gewählt werden, z. B. \(x = a, a+1, \ldots, b\), wobei \(a\) und \(b\) ganze Zahlen sind und \(a \leq b\). Die Anzahl der Werte ist \(n = b - a + 1\), und die Wahrscheinlichkeitsfunktion lautet:
\[P(X = x) = \frac{1}{b - a + 1}, \quad \text{für } x = a, a+1, \ldots, b.\]
Wir notieren \(X \sim \text{DU}(a, b)\) für die diskrete Gleichverteilung auf \([a, b]\).
Figure 4.4 zeigt die Verteilung für \(a = 3\) und \(b = 8\) (z. B. ein modifizierter Würfel). Dieses flexible Intervall ist nützlich, um spezifische Szenarien zu modellieren, z. B. in Simulationen mit nicht standardisierten Bereichen.
import numpy as np
import matplotlib.pyplot as plt
n = 6
x = np.arange(1, n + 1)
P_X = np.full(n, 1/n) # Array mit konstanter Wahrscheinlichkeit 1/n
plt.bar(x, P_X, color='skyblue', width=0.8)
plt.xlabel('Würfelzahl ($X$)')
plt.ylabel('Wahrscheinlichkeit')
plt.title(f'Diskrete Gleichverteilung ($n = {n}$)')
plt.xticks(x)
plt.grid(axis='y', alpha=0.3)
plt.show()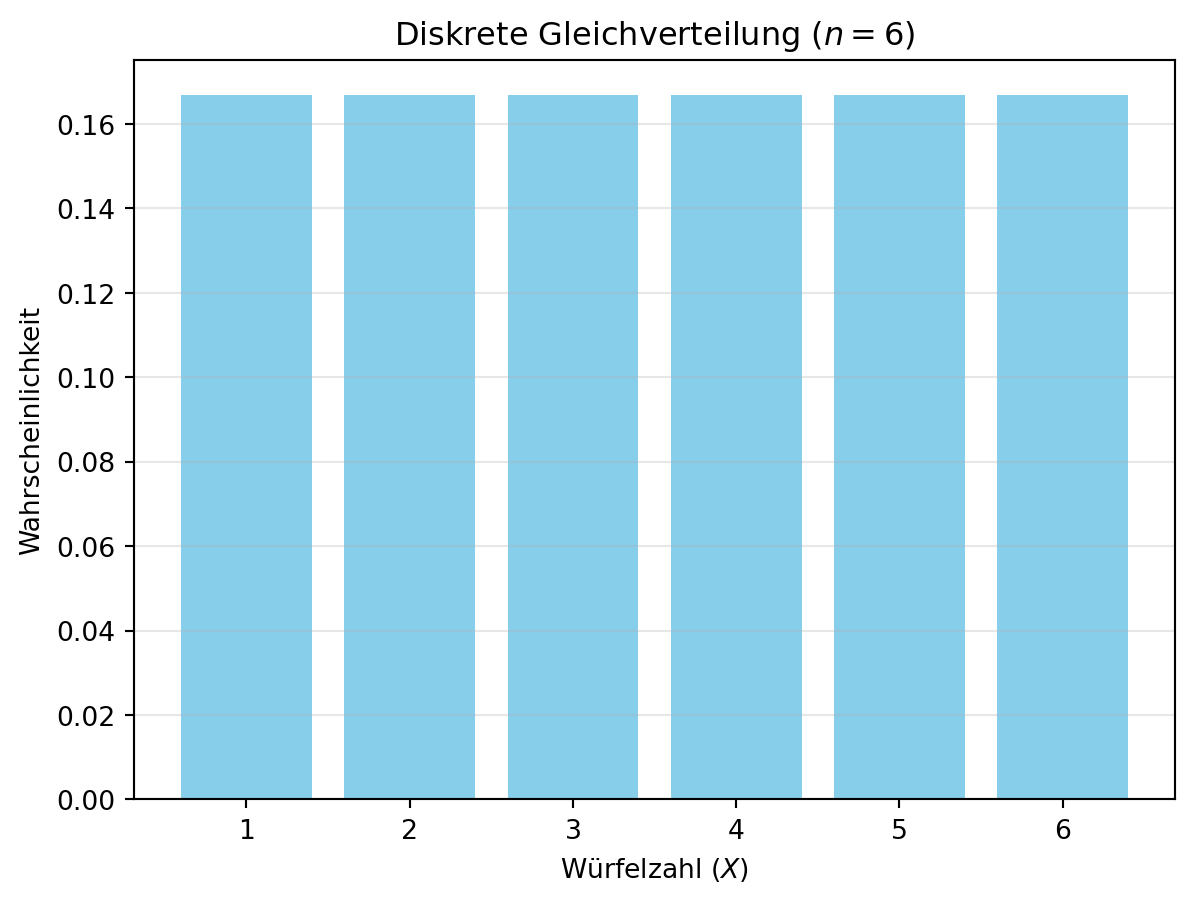
In der Abbildung (fig:sec-dataexploratory-distributions-discrete-uniform-distribution?) wird die Wahrscheinlichkeitsverteilung der diskreten Gleichverteilung für das Würfeln eines Würfels dargestellt. Die Wahrscheinlichkeitsverteilung zeigt, dass alle möglichen Werte der Zufallsvariablen die gleiche Wahrscheinlichkeit haben.
4.1.3.1 Erwartungswert und Varianz der diskreten Gleichverteilung
Der Erwartungswert \(E(X)\) einer diskreten Gleichverteilung auf dem Intervall \([a, b]\) liegt in der Mitte des Intervalls:
\[E(X) = \frac{a + b}{2} = \sum_{x} x \cdot P(X = x).$.\]
Für \(a = 3\) und \(b = 8\) ergibt sich:
\[E(X) = \frac{3 + 8}{2} = 5.5.\]
Die Varianz \(\text{Var}(X)\) beschreibt die Streuung der Verteilung:
\[\text{Var}(X) = \frac{(b - a + 1)^2 - 1}{12} = \sum_{x} (x - E(X))^2 \cdot P(X = x)..\]
Bei \(a = 3\) und \(b = 8\) ist \(n = b - a + 1 = 6\), also:
\[\text{Var}(X) = \frac{6^2 - 1}{12} = \frac{36 - 1}{12} = \frac{35}{12} \approx 2.9167.\]
Diese Formeln gelten für jedes Intervall \([a, b]\), wobei \(a\) und \(b\) ganze Zahlen sind und \(a \leq b\).
4.2 Stetige Verteilungen
Stetige Verteilungen modellieren Zufallsvariablen, die kontinuierliche Werte annehmen können, z. B. Zeit oder Länge. Im Gegensatz zu diskreten Verteilungen gibt es hier unendlich viele mögliche Werte innerhalb eines Intervalls. Wir betrachten die Normalverteilung, Exponentialverteilung und stetige Gleichverteilung, die in Simulationen wie im Tutorial zur Fahrzeugausfallzeit eine Rolle spielen.
4.2.1 Stetige Gleichverteilung
Die stetige Gleichverteilung beschreibt eine Zufallsvariable, bei der alle Werte in einem Intervall \([a, b]\) gleich wahrscheinlich sind. Die Wahrscheinlichkeitsdichtefunktion (Dichte) lautet:
\[f(x) = \begin{cases}
\frac{1}{b - a} & \text{für } a \leq x \leq b, \\
0 & \text{sonst}.
\end{cases}\]
Wir schreiben \(X \sim \text{U}(a, b)\). Bei stetigen Verteilungen wird die Wahrscheinlichkeit als Fläche unter der Dichte berechnet, wobei die Gesamtfläche stets 1 beträgt.
Figure 4.5 zeigt die Dichte für \(a = 0\) und \(b = 1\). Im Tutorial wird die stetige Gleichverteilung für die Steuereinheit (\(X \sim \text{U}(4000, 8000)\)) verwendet, um Ausfallzeiten zu modellieren.
import numpy as np
import matplotlib.pyplot as plt
a = 0
b = 1
x = np.linspace(a - 0.5, b + 0.5, 1000)
f_X = np.where((x >= a) & (x <= b), 1 / (b - a), 0)
plt.plot(x, f_X, color='skyblue', linewidth=2)
plt.fill_between(x, f_X, alpha=0.2, color='skyblue') # Fläche einfärben
plt.xlabel('Werte der Zufallsvariablen ($X$)')
plt.ylabel('Wahrscheinlichkeitsdichte')
plt.title(f'Stetige Gleichverteilung ($a = {a}$, $b = {b}$)')
plt.grid(alpha=0.3)
plt.show()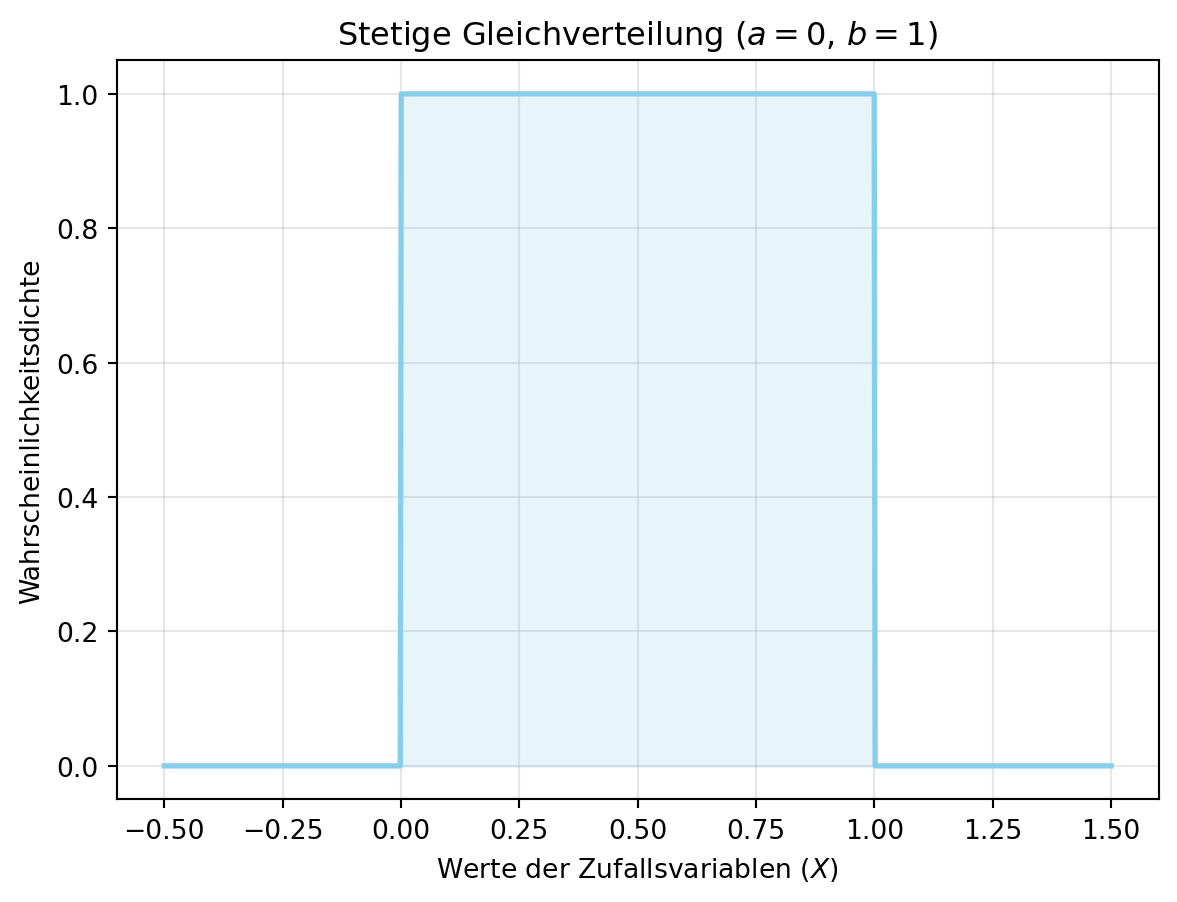
Bei stetigen Verteilungen ist die Wahrscheinlichkeit eines exakten Wertes 0, da es unendlich viele mögliche Werte gibt. Stattdessen berechnen wir die Wahrscheinlichkeit für einen Wertebereich als Fläche unter der Dichtefunktion:
\[P(a \leq X \leq b) = \int_{a}^{b} f(x) \, dx.\]
Der Erwartungswert \(E(X)\) einer gleichverteilten Zufallsvariable \(X \sim \text{U}(a, b)\) ist:
\[E(X) = \frac{a + b}{2}=\int\limits_{ - \infty }^\infty {x \cdot f\left( x \right)} \,\,dx.\]
Die Varianz \(\text{Var}(X)\) beträgt:
\[\text{Var}(X) = \frac{(b - a)^2}{12} = \int\limits_{ - \infty }^\infty {{{\left( {x - {\mu _x}} \right)}^2}} \cdot f\left( x \right)\,\,dx.\]
4.2.1.1 Beispiel: Ausfallwahrscheinlichkeit eines Bauteils
Der Ausfall eines elektronischen Bauteils folgt einer stetigen Gleichverteilung auf \([0, 3650]\) Tagen (\(X \sim \text{U}(0, 3650)\)). Wie hoch ist die Wahrscheinlichkeit, dass es innerhalb der ersten 1000 Tage ausfällt?
Die Dichtefunktion ist:
\[f(x) = \begin{cases}
\frac{1}{3650 - 0} = \frac{1}{3650} & \text{für } 0 \leq x \leq 3650, \\
0 & \text{sonst}.
\end{cases}\]
Die Wahrscheinlichkeit ergibt sich durch Integration:
\[P(0 \leq X \leq 1000) = \int_{0}^{1000} \frac{1}{3650} \, dx = \frac{1000}{3650} \approx 0.274.\]
Das Bauteil hat also eine 27,4 % Chance, innerhalb von 1000 Tagen auszusetzen. Dieses Prinzip wird im Tutorial bei der Steuereinheit (\(X \sim \text{U}(4000, 8000)\)) angewendet.
- Dichte: \(f(x) = \frac{1}{3650}\) für \(0 \leq x \leq 3650\).
- Integral: \(P(0 \leq X \leq 1000) = \int_{0}^{1000} \frac{1}{3650} \, dx\).
- Ergebnis: \(\frac{1000}{3650} = 0.274\).
4.2.2 Normalverteilung
Die Normalverteilung ist eine stetige Verteilung, die in Statistik und Naturwissenschaften weit verbreitet ist. Ihre Glockenform zeigt eine symmetrische Verteilung der Werte um den Erwartungswert. Die Dichtefunktion lautet:
\[f(x) = \frac{1}{\sqrt{2\pi} \sigma} \exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right),\]
für \(-\infty < x < \infty\). Wir schreiben \(X \sim \mathcal{N}(\mu, \sigma^2)\), wobei \(\mu\) der Erwartungswert und \(\sigma^2\) die Varianz ist.
Falls \(\mu = 0\) und \(\sigma = 1\), spricht man von der Standardnormalverteilung (\(X \sim \mathcal{N}(0, 1)\)), eine spezielle Form mit Erwartungswert 0 und Varianz 1. Figure 4.6 zeigt diese Verteilung. Im Tutorial wird die Normalverteilung für den Sensor (\(X \sim \mathcal{N}(6000, 100^2)\)) genutzt, um Ausfallzeiten zu modellieren.
import numpy as np
import matplotlib.pyplot as plt
mu = 0
sigma = 1
x = np.linspace(-5, 5, 1000)
f_X = 1 / (np.sqrt(2 * np.pi) * sigma) * np.exp(-((x - mu) ** 2) / (2 * sigma ** 2))
plt.plot(x, f_X, color='skyblue', linewidth=2)
plt.fill_between(x, f_X, alpha=0.2, color='skyblue') # Fläche einfärben
plt.xlabel('Werte der Zufallsvariablen ($X$)')
plt.ylabel('Wahrscheinlichkeitsdichte')
plt.title(f'Standardnormalverteilung ($\mu = {mu}$, $\sigma = {sigma}$)')
plt.grid(alpha=0.3)
plt.show()<>:13: SyntaxWarning:
invalid escape sequence '\m'
<>:13: SyntaxWarning:
invalid escape sequence '\s'
<>:13: SyntaxWarning:
invalid escape sequence '\m'
<>:13: SyntaxWarning:
invalid escape sequence '\s'
/tmp/ipykernel_3243/513147542.py:13: SyntaxWarning:
invalid escape sequence '\m'
/tmp/ipykernel_3243/513147542.py:13: SyntaxWarning:
invalid escape sequence '\s'
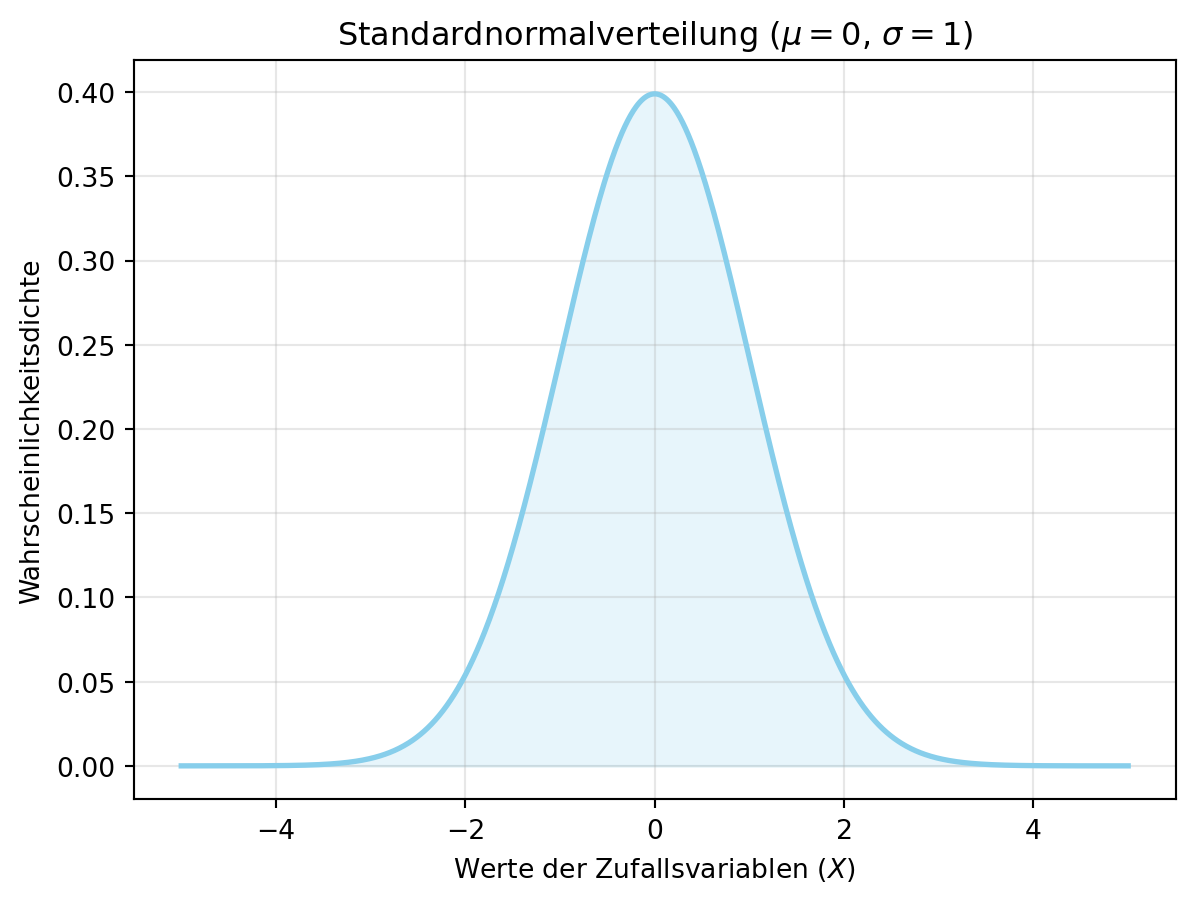
Früher, ohne Computer, war die Berechnung der Fläche unter der Normalverteilungskurve (\(P(X \leq x)\)) schwierig. Man nutzte \(Z\)-Wert-Tabellen, um die Wahrscheinlichkeit für eine standardnormalverteilte Zufallsvariable \(Z \sim \mathcal{N}(0, 1)\) nachzuschlagen. Beispiele:
- \(P(Z \leq 0) = 0.5\) (50 %).
- \(P(Z \leq 1) = 0.8413\) (84,13 %).
- \(P(Z \leq -1) = 1 - P(Z \leq 1) = 0.1587\) (15,87 %).
Umgekehrt: \(P(Z \leq 1.645) = 0.95\) (95 %). Heute ersetzen Computerprogramme solche Tabellen, wie im Folgenden gezeigt.
4.2.2.1 Erwartungswert und Varianz der Normalverteilung
Der Erwartungswert \(E(X)\) einer normalverteilten Zufallsvariable \(X \sim \mathcal{N}(\mu, \sigma^2)\) ist:
\[E(X) = \mu = \int\limits_{ - \infty }^\infty {x \cdot f\left( x \right)} \,\,dx.\]
Die Varianz \(\text{Var}(X)\) beträgt:
\[{\sigma _x}^2 = Var\left( X \right) = E{\left( {X - {\mu _x}} \right)^2} = \int\limits_{ - \infty }^\infty {{{\left( {x - {\mu _x}} \right)}^2}} \cdot f\left( x \right)\,\,dx.\]
Für die Standardnormalverteilung (\(X \sim \mathcal{N}(0, 1)\)) gilt \(E(X) = 0\) und \(\text{Var}(X) = 1\). Im Tutorial wird dies für den Sensor (\(X \sim \mathcal{N}(6000, 100^2)\)) genutzt.
4.2.2.1.1 Standardisierung der Normalverteilung
Viele Zufallsvariablen folgen keiner Standardnormalverteilung, sondern haben andere Werte für \(\mu\) und \(\sigma\). Um diese auf \(Z \sim \mathcal{N}(0, 1)\) zu überführen, wird standardisiert:
\[Z = \frac{X - \mu}{\sigma}.\]
\(Z\) hat dann \(E(Z) = 0\) und \(\text{Var}(Z) = 1\), sodass \(Z\)-Tabellen oder Software genutzt werden können.
4.2.2.2 Beispiel: Intelligenz-Quotient (IQ)
Der IQ ist normalverteilt mit \(X \sim \mathcal{N}(100, 15^2)\) (\(\mu = 100\), \(\sigma = 15\)). Wie wahrscheinlich ist ein IQ von 130 oder mehr (\(P(X \geq 130)\))?
4.2.2.2.1 Analytische Berechnung
Die Dichtefunktion ist:
\[f(x) = \frac{1}{\sqrt{2\pi} \cdot 15} \exp\left(-\frac{(x - 100)^2}{2 \cdot 15^2}\right).\]
Die Wahrscheinlichkeit \(P(X \geq 130)\) ergibt sich als:
\[P(X \geq 130) = 1 - P(X \leq 130) = 1 - \int_{-\infty}^{130} f(x) \, dx.\]
Mit Standardisierung:
\[Z = \frac{130 - 100}{15} = 2, \quad P(X \leq 130) = P(Z \leq 2).\]
Aus Tabellen oder Software: \(P(Z \leq 2) \approx 0.9772\), also:
\[P(X \geq 130) = 1 - 0.9772 = 0.0228 \text{ (2,28 %)}.\]
4.2.2.2.2 Berechnung mit Python
Mit scipy.stats.norm können wir die kumulative Verteilungsfunktion (cdf) direkt berechnen:
import numpy as np
from scipy.stats import norm
mu = 100
sigma = 15
P_X_geq_130 = 1 - norm.cdf(130, loc=mu, scale=sigma)
print(f'P(X >= 130) = {P_X_geq_130:.4f}') # Ausgabe: 0.0228P(X >= 130) = 0.02284.2.2.3 Visualisierung der Wahrscheinlichkeiten
Oft interessiert der Anteil einer Population innerhalb von ein oder zwei Standardabweichungen vom Mittelwert. Für eine normalverteilte Zufallsvariable \(X \sim \mathcal{N}(\mu, \sigma^2)\) berechnen wir:
\[P(\mu - \sigma \leq X \leq \mu + \sigma) = P(X \leq \mu + \sigma) - P(X \leq \mu - \sigma),\]
wobei \(P(X \leq x)\) die kumulative Verteilungsfunktion (CDF) ist. Für die Standardnormalverteilung gilt:
- \(P(\mu - \sigma \leq X \leq \mu + \sigma) \approx 0.6826\) (ca. 68 %),
- \(P(\mu - 2\sigma \leq X \leq \mu + 2\sigma) \approx 0.9544\) (ca. 95 %).
Im IQ-Beispiel (\(X \sim \mathcal{N}(100, 15^2)\)) prüfen wir den Bereich von zwei Standardabweichungen (\(\mu - 2\sigma = 70\), \(\mu + 2\sigma = 130\)). Figure 4.8 zeigt diese Wahrscheinlichkeit. Solche Berechnungen sind im Tutorial nützlich, z. B. um Sensor-Ausfallzeiten zu analysieren.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
mu = 100
sigma = 15
x = np.linspace(mu - 4*sigma, mu + 4*sigma, 1000)
f_X = norm.pdf(x, loc=mu, scale=sigma)
# Wahrscheinlichkeit für μ ± 2σ
P_X_2_sigma = norm.cdf(mu + 2*sigma, loc=mu, scale=sigma) - norm.cdf(mu - 2*sigma, loc=mu, scale=sigma)
print(f'P({mu - 2*sigma} <= X <= {mu + 2*sigma}) = {P_X_2_sigma:.4f}') # Ausgabe: 0.9545
# Plot
plt.plot(x, f_X, color='skyblue', linewidth=2)
plt.fill_between(x, f_X, where=(x >= mu - 2*sigma) & (x <= mu + 2*sigma), color='lightblue', alpha=0.3, label=f'P = {P_X_2_sigma:.4f}')
plt.axvline(mu - 2*sigma, color='red', linestyle='--', label=f'{mu - 2*sigma}')
plt.axvline(mu + 2*sigma, color='red', linestyle='--', label=f'{mu + 2*sigma}')
plt.xlabel('IQ-Wert ($X$)')
plt.ylabel('Wahrscheinlichkeitsdichte')
plt.title(f'IQ-Verteilung ($\mu = {mu}$, $\sigma = {sigma}$)')
plt.legend()
plt.grid(alpha=0.3)
plt.show()<>:21: SyntaxWarning:
invalid escape sequence '\m'
<>:21: SyntaxWarning:
invalid escape sequence '\s'
<>:21: SyntaxWarning:
invalid escape sequence '\m'
<>:21: SyntaxWarning:
invalid escape sequence '\s'
/tmp/ipykernel_3243/3074097218.py:21: SyntaxWarning:
invalid escape sequence '\m'
/tmp/ipykernel_3243/3074097218.py:21: SyntaxWarning:
invalid escape sequence '\s'
P(70 <= X <= 130) = 0.9545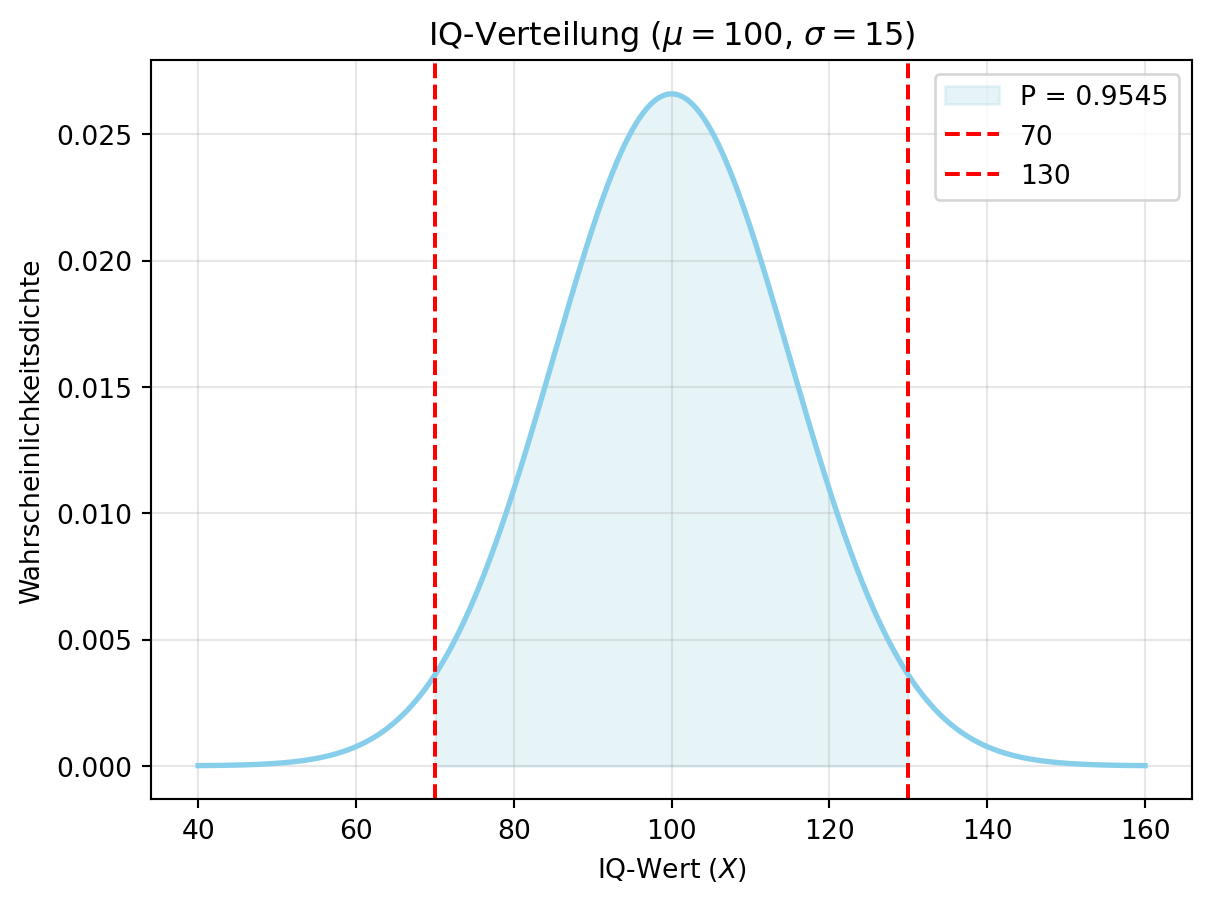
Der IQ ist so skaliert, dass \(\mu = 100\) und \(\sigma = 15\). Die Wahrscheinlichkeit für einen IQ \(\geq 130\) beträgt etwa 2,28 %, während 95,45 % der Bevölkerung einen IQ zwischen 70 und 130 haben (innerhalb von \(\pm 2\sigma\)). Dies zeigt die praktische Relevanz der Normalverteilung.
4.3 Weitere Verteilungen
Neben der Normalverteilung spielen weitere stetige und diskrete Verteilungen eine Rolle in Statistik und Simulationen, wie im Tutorial zur Fahrzeugausfallzeit genutzt:
- Die Exponentialverteilung modelliert die Zeit zwischen unabhängigen Ereignissen, z. B. in der Zuverlässigkeitsanalyse oder Warteschlangentheorie.
- Die Poissonverteilung (diskret) beschreibt die Anzahl von Ereignissen in einem festen Zeitintervall, etwa in Zufallsprozessen.
Diese Verteilungen sind im Python-Modul scipy.stats verfügbar, das Funktionen für Wahrscheinlichkeiten und Zufallszahlen bietet. Im Tutorial wird z. B. die Poissonverteilung für den Motor (\(X \sim \text{Poisson}(5000)\)) eingesetzt.
4.3.1 Exponentialverteilung
Die Dichtefunktion der Exponentialverteilung ist:
\[f(x) = \lambda e^{-\lambda x}, \quad x \geq 0,\]
wobei \(\lambda\) die Rate ist. Wir schreiben \(X \sim \text{Exp}(\lambda)\), mit \(E(X) = \frac{1}{\lambda}\) und \(\text{Var}(X) = \frac{1}{\lambda^2}\). Sie ist im Tutorial für Ausfallzeiten relevant, wenn Ereignisse exponentiell verteilt wären.
4.4 Fitting von Verteilungen
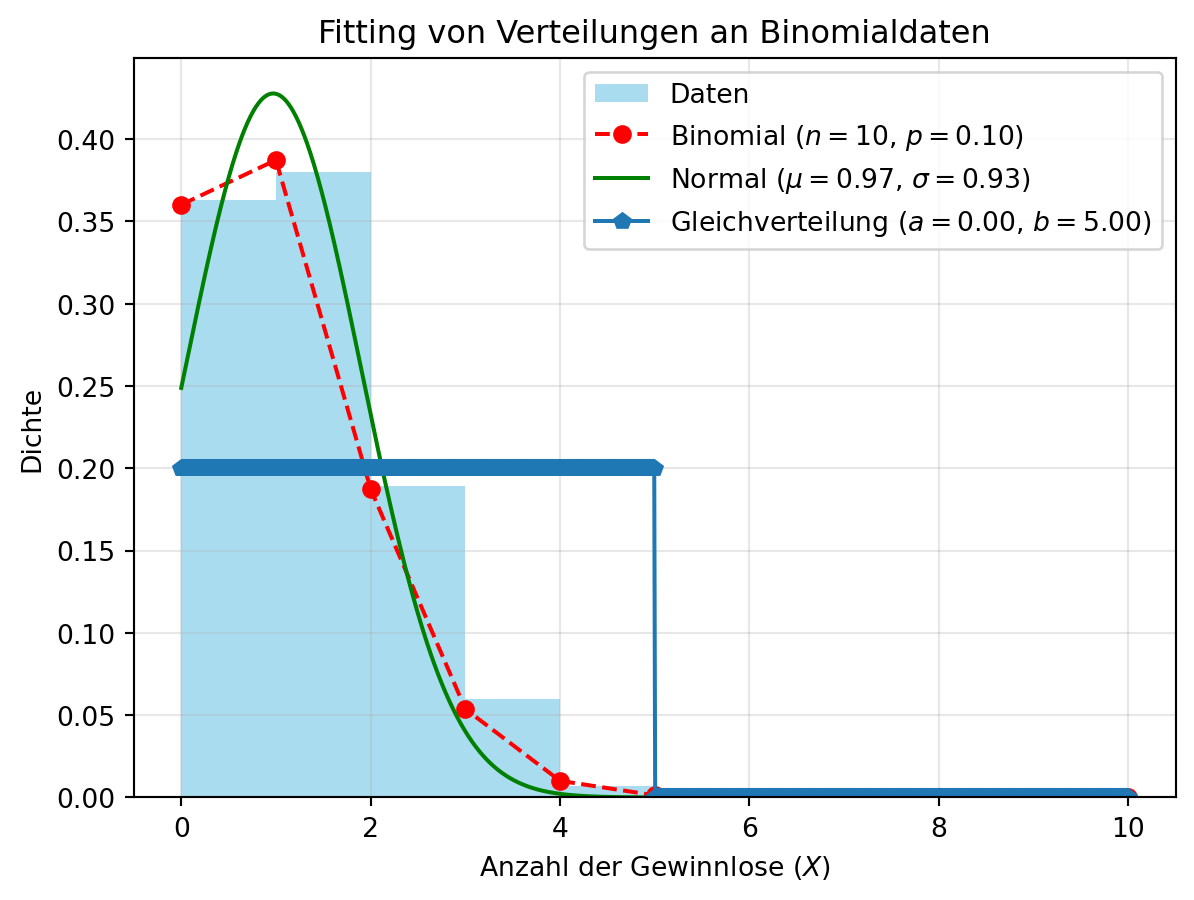
In der Praxis müssen wir oft die Verteilung von Daten bestimmen – ein Prozess namens Fitting. Ziel ist es, die Verteilung zu finden, die die Daten am besten beschreibt. Methoden wie Maximum-Likelihood-Schätzung oder die Methode der Momente werden dafür genutzt.
Als Beispiel simulieren wir Lotterie-Daten mit \(X \sim \text{Bin}(10, 0.1)\) und passen verschiedene Verteilungen an, um zu vergleichen, welche die Daten am besten modelliert.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom, norm, uniform
np.random.seed(42)
data = np.random.binomial(n=10, p=0.1, size=1000) # 1000 Ziehungen
# Binomialverteilung schätzen
n_est = 10 # Bekannt aus Simulation
p_est = np.mean(data) / n_est
binom_x = np.arange(0, n_est + 1)
binom_y = binom.pmf(binom_x, n=n_est, p=p_est)
# Normalverteilung schätzen
mu, sigma = norm.fit(data)
norm_x = np.linspace(0, 10, 1000)
norm_y = norm.pdf(norm_x, mu, sigma)
# Gleichverteilung schätzen
a, b = uniform.fit(data)
uniform_x = np.linspace(0, 10, 1000)
uniform_y = uniform.pdf(uniform_x, a, b - a)
# Plot
plt.hist(data, bins=range(11), density=True, color='skyblue', alpha=0.7, label='Daten')
plt.plot(binom_x, binom_y, 'ro--', label=f'Binomial ($n={n_est}$, $p={p_est:.2f}$)')
plt.plot(norm_x, norm_y, 'g-', label=f'Normal ($\mu={mu:.2f}$, $\sigma={sigma:.2f}$)')
plt.plot(uniform_x, uniform_y, 'p-', label=f'Gleichverteilung ($a={a:.2f}$, $b={b:.2f}$)')
plt.xlabel('Anzahl der Gewinnlose ($X$)')
plt.ylabel('Dichte')
plt.title('Fitting von Verteilungen an Binomialdaten')
plt.legend()
plt.grid(alpha=0.3)
plt.show()<>:27: SyntaxWarning:
invalid escape sequence '\m'
<>:27: SyntaxWarning:
invalid escape sequence '\s'
<>:27: SyntaxWarning:
invalid escape sequence '\m'
<>:27: SyntaxWarning:
invalid escape sequence '\s'
/tmp/ipykernel_3243/1255964559.py:27: SyntaxWarning:
invalid escape sequence '\m'
/tmp/ipykernel_3243/1255964559.py:27: SyntaxWarning:
invalid escape sequence '\s'
4.5 Rechnen mit Verteilungen, Zufallsvariablen und Erwartungswert
Der zentrale Grenzwertsatz besagt, dass die Summe einer großen Anzahl von unabhängigen und identisch verteilten (i.i.d.) Zufallsvariablen einer Normalverteilung folgt – unabhängig von ihrer ursprünglichen Verteilung. Dies ist ein Grundpfeiler der Statistik und erklärt, warum Normalverteilungen in Simulationen wie im Tutorial oft auftreten.
4.5.1 Rechenregeln für Erwartungswert und Varianz
Für unabhängige Zufallsvariablen \(X_1, X_2, \ldots, X_n\) gelten folgende Regeln:
Erwartungswert: Die Summe der Erwartungswerte gilt immer, auch ohne Unabhängigkeit:
\[E(X_1 + X_2 + \cdots + X_n) = E(X_1) + E(X_2) + \cdots + E(X_n).\]Varianz: Bei Unabhängigkeit (Kovarianz = 0) ist die Varianz die Summe der Varianzen:
\[\text{Var}(X_1 + X_2 + \cdots + X_n) = \text{Var}(X_1) + \text{Var}(X_2) + \cdots + \text{Var}(X_n).\]
Andernfalls: \(\text{Var}(X_1 + X_2) = \text{Var}(X_1) + \text{Var}(X_2) + 2 \text{Cov}(X_1, X_2)\).Linearkombinationen: Für \(aX + bY\):
\[E(aX + bY) = aE(X) + bE(Y),\]
\[\text{Var}(aX + bY) = a^2 \text{Var}(X) + b^2 \text{Var}(Y) + 2ab \text{Cov}(X, Y),\]
wobei \(\text{Cov}(X, Y) = 0\) bei Unabhängigkeit.
Die Kovarianz \(\text{Cov}(X, Y)\) misst den linearen Zusammenhang zwischen \(X\) und \(Y\). Bei Unabhängigkeit ist sie 0, was die Varianzberechnung vereinfacht.
4.5.2 Beispiel: Summe von Zufallsvariablen aus verschiedenen Verteilungen
Der zentrale Grenzwertsatz gilt auch, wenn die Zufallsvariablen nicht identisch verteilt sind, solange sie unabhängig sind und die Anzahl groß ist. Figure 4.10 zeigt, wie die Summe von Uniform-, Exponential- und Binomialverteilungen einer Normalverteilung ähnelt – ein Prinzip, das in Monte-Carlo-Simulationen wie im Tutorial genutzt wird.
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
N = 10000
# Zufallsvariablen definieren
X_uni_1 = np.random.uniform(0, 10, N) # Uniform [0, 10]
X_uni_2 = np.random.uniform(2, 8, N) # Uniform [2, 8]
X_exp_1 = np.random.exponential(2, N) # Exponential, Scale = 2
X_exp_2 = np.random.exponential(3, N) # Exponential, Scale = 3
X_bin_1 = np.random.binomial(20, 0.3, N) # Binomial (n=20, p=0.3)
X_bin_2 = np.random.binomial(15, 0.4, N) # Binomial (n=15, p=0.4)
X_sum = X_uni_1 + X_uni_2 + X_exp_1 + X_exp_2 + X_bin_1 + X_bin_2
# Plot
plt.figure(figsize=(12, 6))
plt.hist(X_sum, bins=50, density=True, color='skyblue', alpha=0.7, label='Summe')
plt.hist(X_uni_1, bins=50, density=True, alpha=0.3, label='Uniform 1')
plt.hist(X_uni_2, bins=50, density=True, alpha=0.3, label='Uniform 2')
plt.hist(X_exp_1, bins=50, density=True, alpha=0.3, label='Exponential 1')
plt.hist(X_exp_2, bins=50, density=True, alpha=0.3, label='Exponential 2')
plt.hist(X_bin_1, bins=50, density=True, alpha=0.3, label='Binomial 1')
plt.hist(X_bin_2, bins=50, density=True, alpha=0.3, label='Binomial 2')
plt.xlabel('Wert')
plt.ylabel('Dichte')
plt.title('Summe von Zufallsvariablen aus verschiedenen Verteilungen')
plt.legend()
plt.grid(alpha=0.3)
plt.show()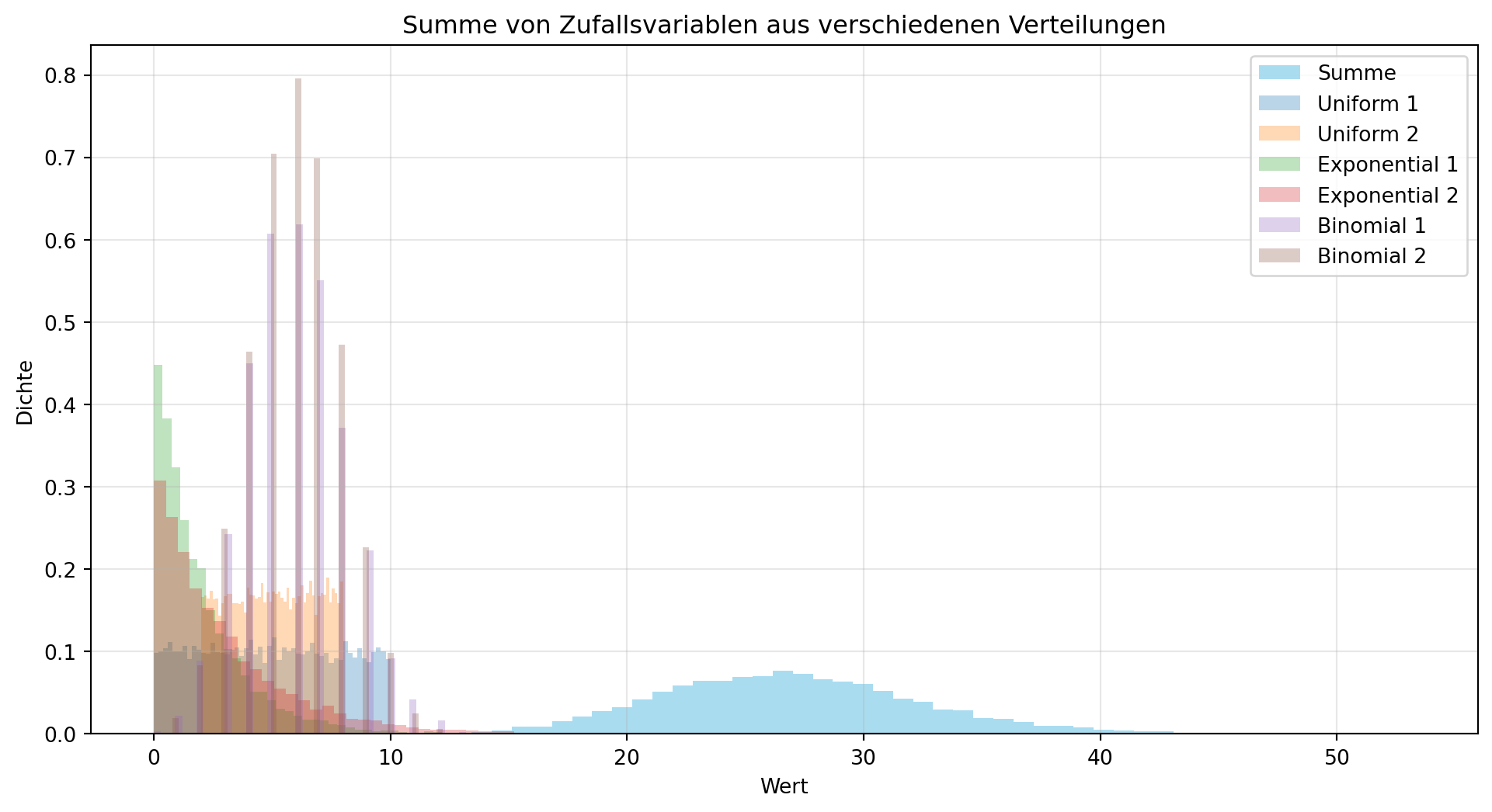
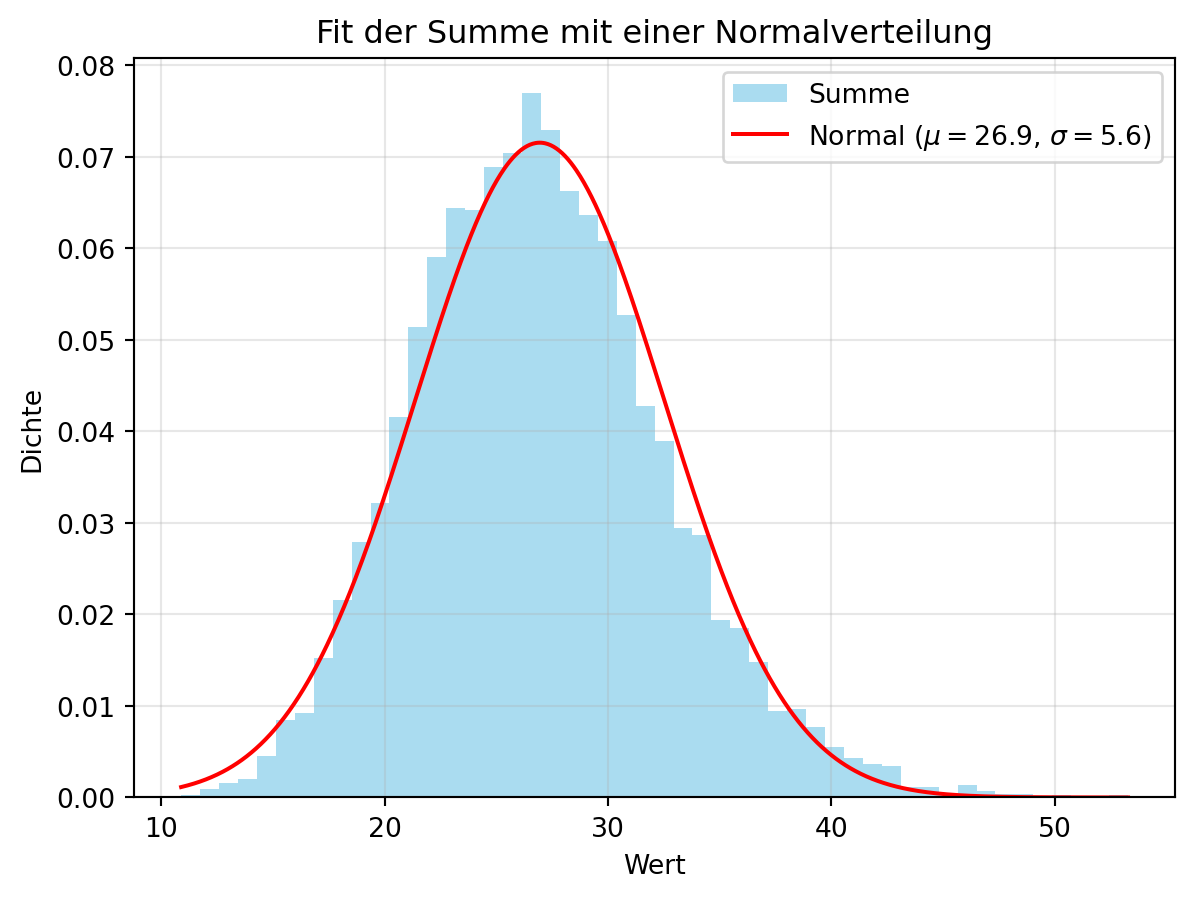
4.5.2.1 Normalverteilungs-Fit der Summe
Um den zentralen Grenzwertsatz zu veranschaulichen, passen wir eine Normalverteilung an die Summe an. Figure 4.11 zeigt, wie gut die Summe einer Normalverteilung entspricht.
from scipy.stats import norm
# Normalverteilung an Summe anpassen
X_sum_mu, X_sum_sigma = norm.fit(X_sum)
# Plot
plt.hist(X_sum, bins=50, density=True, color='skyblue', alpha=0.7, label='Summe')
x = np.linspace(min(X_sum), max(X_sum), 1000)
y = norm.pdf(x, X_sum_mu, X_sum_sigma)
plt.plot(x, y, 'r-', label=f'Normal ($\mu={X_sum_mu:.1f}$, $\sigma={X_sum_sigma:.1f}$)')
plt.xlabel('Wert')
plt.ylabel('Dichte')
plt.title('Fit der Summe mit einer Normalverteilung')
plt.legend()
plt.grid(alpha=0.3)
plt.show()<>:10: SyntaxWarning:
invalid escape sequence '\m'
<>:10: SyntaxWarning:
invalid escape sequence '\s'
<>:10: SyntaxWarning:
invalid escape sequence '\m'
<>:10: SyntaxWarning:
invalid escape sequence '\s'
/tmp/ipykernel_3243/3238649060.py:10: SyntaxWarning:
invalid escape sequence '\m'
/tmp/ipykernel_3243/3238649060.py:10: SyntaxWarning:
invalid escape sequence '\s'