8  Erweiterungen der Linearen Regression

Zusammenhänge können auch zwischen mehr als zwei Variablen bestehen. In diesem Fall sprechen wir von einer multiplen linearen Regression. Das Modell kann dann wie folgt formuliert werden:

\[ Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \ldots + \beta_p X_p + \epsilon \]

Als Beispiel könnten wir nicht nur die Absatzmenge eines Produkts in Abhängigkeit von der Werbeausgabe für TV-Spots, sondern auch von der Werbeausgabe für Radio-Spots modellieren. Wir simuliieren die Daten wieder mit Python, so dass wir die Zusammenhänge kennen.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

# Simulate population data
np.random.seed(0)
X_1 = 300 * np.random.rand(100, 1)
X_2 = 100 * np.random.rand(100, 1)
X_3 = 200 * np.random.rand(100, 1)

Y = 7 + 0.05 * X_1 + 0.1 * X_2 + 0.2 * X_3 + 5 * np.random.randn(100, 1) +  0.1 * X_1 * X_2

# Simulate sample data
sample_size = 100
idx = np.random.choice(100, sample_size, replace=False)
X_sample = [X_1[idx], X_2[idx], X_3[idx]]
Y_sample = Y[idx]

# Store data in a tidy dataframe
data = pd.DataFrame({"X_1 (TV advertising spending (€))": X_sample[0].flatten(), "X_2 (Radio advertising spending (€))": X_sample[1].flatten(), "X_3 (Newspaper advertising spending (€))": X_sample[2].flatten(), "Y (Sales)": Y_sample.flatten()})
print(data.head())
   X_1 (TV advertising spending (€))  X_2 (Radio advertising spending (€))  \
0                         261.003644                             69.253159   
1                         138.443809                             95.608363   
2                         156.554497                             66.017354   
3                         207.741636                             23.789282   
4                          79.616847                             61.396596   

   X_3 (Newspaper advertising spending (€))    Y (Sales)  
0                                166.209691  1859.370107  
1                                 54.708407  1353.996485  
2                                189.474118  1096.313335  
3                                  2.647372   513.700056  
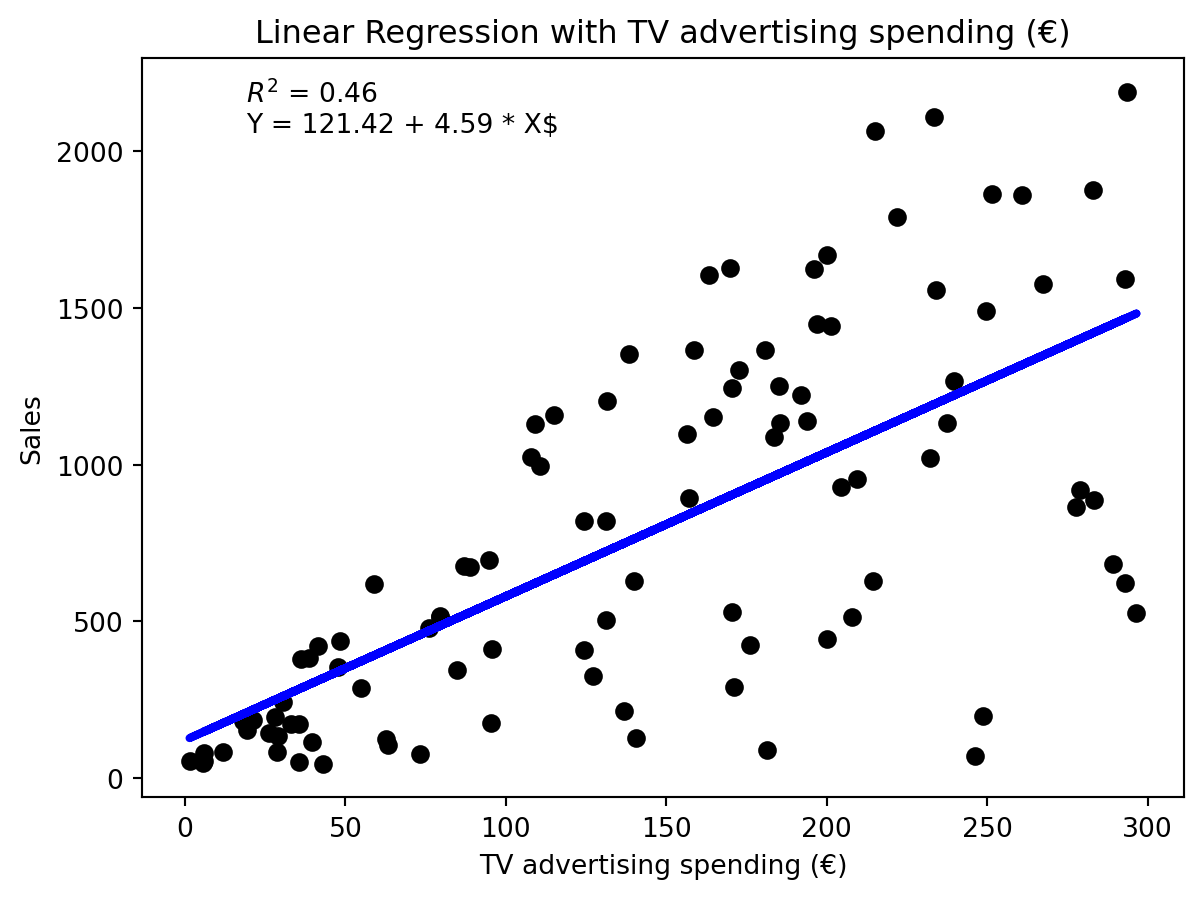
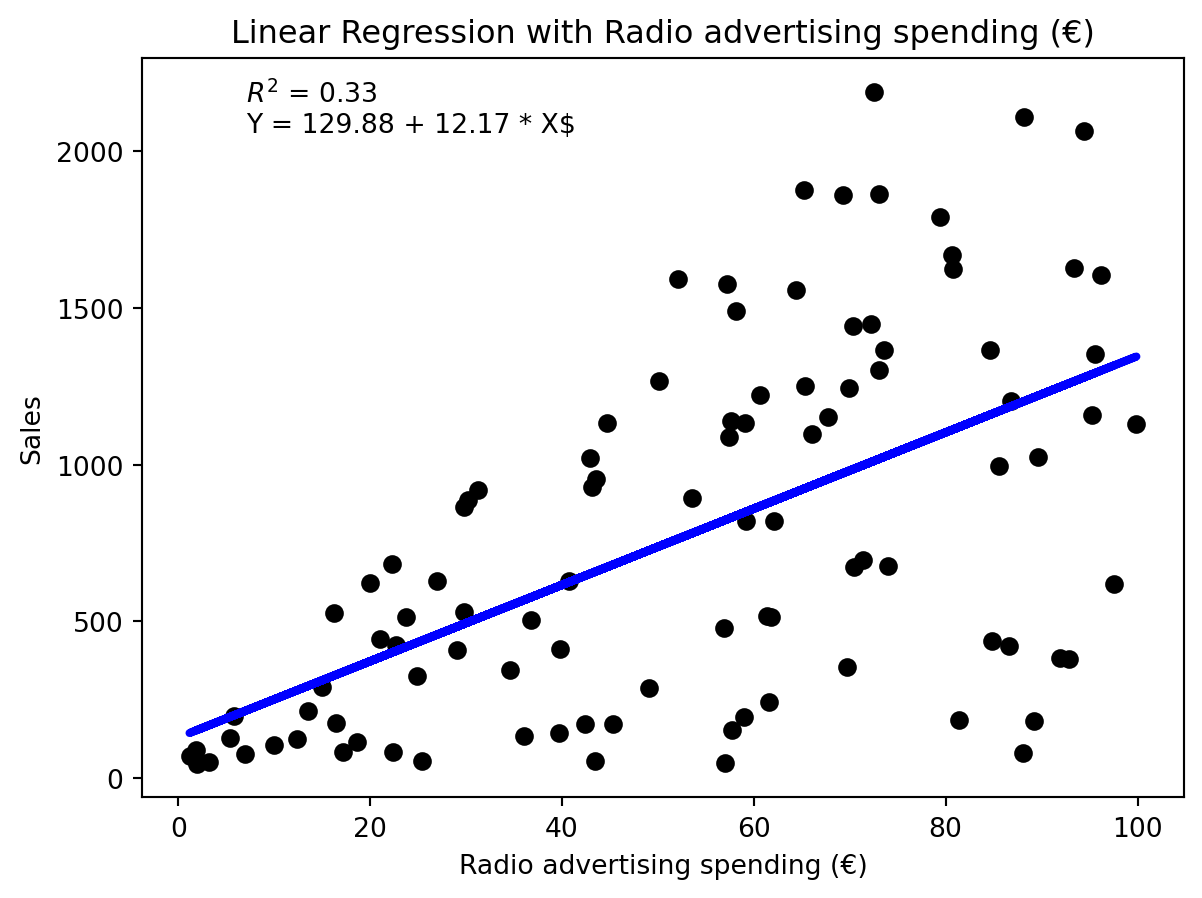
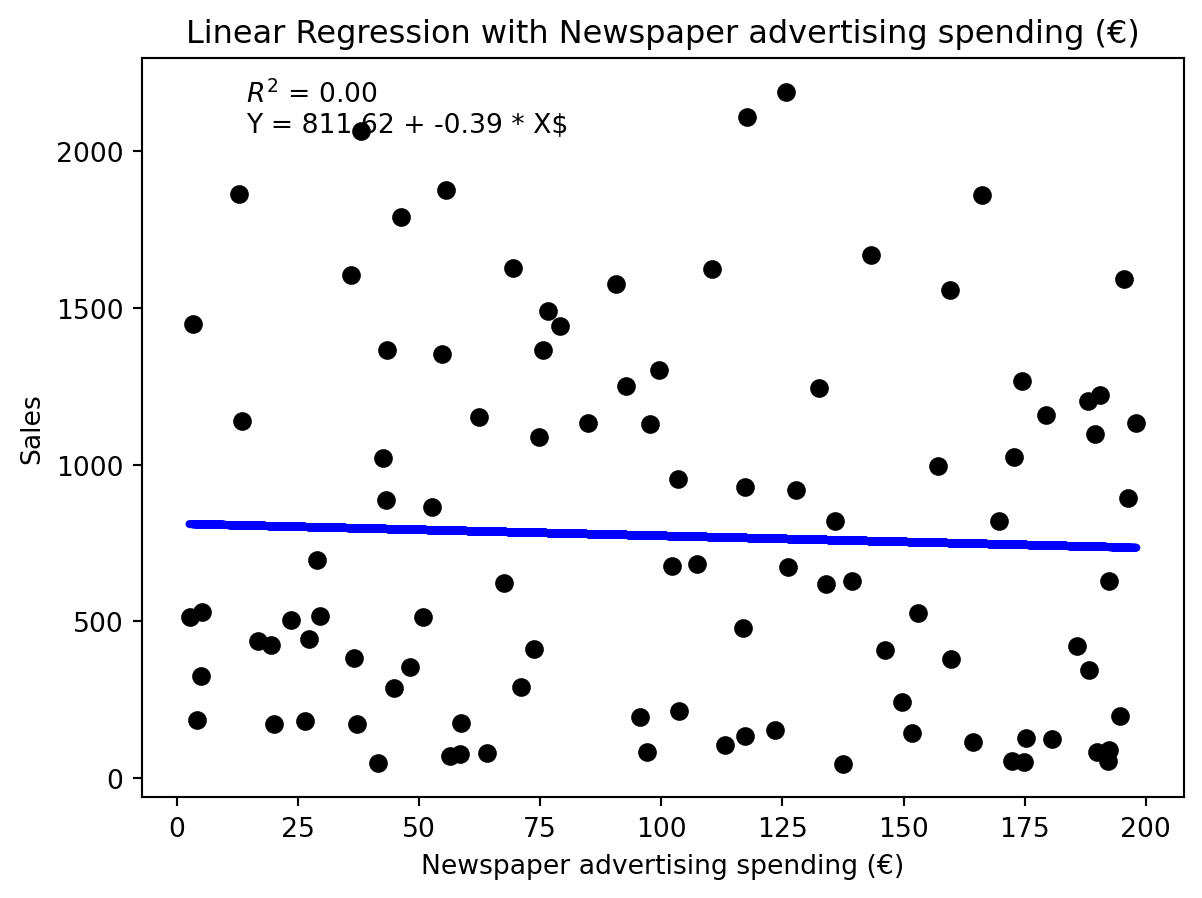
4                                 29.628172   517.255193

Wir können nun drei unabhängige Modelle fitten und visualisieren.

from sklearn.linear_model import LinearRegression

labels = ["TV advertising spending (€)", "Radio advertising spending (€)", "Newspaper advertising spending (€)"]
for predictor in range(3):
    # Fit the model
    model = LinearRegression()
    model.fit(X_sample[predictor].reshape(-1, 1), Y_sample)
    
    # Predict the values
    Y_pred = model.predict(X_sample[predictor].reshape(-1, 1))
    
    # Plot the data
    plt.scatter(X_sample[predictor], Y_sample, color='black')
    plt.plot(X_sample[predictor], Y_pred, color='blue', linewidth=3)
    plt.xlabel(labels[predictor])
    plt.ylabel("Sales")
    plt.title(f"Linear Regression with {labels[predictor]}")
    # Plot R^2
    plt.text(0.1, 0.9, f"$R^2$ = {model.score(X_sample[predictor].reshape(-1, 1), Y_sample):.2f}\nY = {model.intercept_[0]:.2f} + {model.coef_[0][0]:.2f} * X$", transform=plt.gca().transAxes)

    plt.show()

Lineare Regression für die drei unabhängigen Variablen

Lineare Regression für die drei unabhängigen Variablen

Offensichtlich sind die Modelle von mittlerer Qualität. Wir können die drei unabhängigen Variablen auch in einem Modell zusammenfassen.

# Fit the model
import statsmodels.api as sm

# Fit linear regression model
X_sm = sm.add_constant(data[["X_1 (TV advertising spending (€))", "X_2 (Radio advertising spending (€))", "X_3 (Newspaper advertising spending (€))"]])
model_sm = sm.OLS(data["Y (Sales)"], X_sm).fit()

# Get slope and intercept
print(model_sm.summary())
                            OLS Regression Results                            
==============================================================================
Dep. Variable:              Y (Sales)   R-squared:                       0.853
Model:                            OLS   Adj. R-squared:                  0.848
Method:                 Least Squares   F-statistic:                     185.7
Date:                Tue, 24 Jun 2025   Prob (F-statistic):           7.83e-40
Time:                        07:09:55   Log-Likelihood:                -683.06
No. Observations:                 100   AIC:                             1374.
Df Residuals:                      96   BIC:                             1385.
Df Model:                           3                                         
Covariance Type:            nonrobust                                         
============================================================================================================
                                               coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------------------------------------
const                                     -689.7437     78.760     -8.757      0.000    -846.082    -533.406
X_1 (TV advertising spending (€))            4.8871      0.265     18.429      0.000       4.361       5.414
X_2 (Radio advertising spending (€))        13.3451      0.835     15.986      0.000      11.688      15.002
X_3 (Newspaper advertising spending (€))     0.6292      0.382      1.646      0.103      -0.130       1.388
==============================================================================
Omnibus:                        2.763   Durbin-Watson:                   1.906
Prob(Omnibus):                  0.251   Jarque-Bera (JB):                2.632
Skew:                          -0.394   Prob(JB):                        0.268
Kurtosis:                       2.891   Cond. No.                         679.
==============================================================================

Notes:
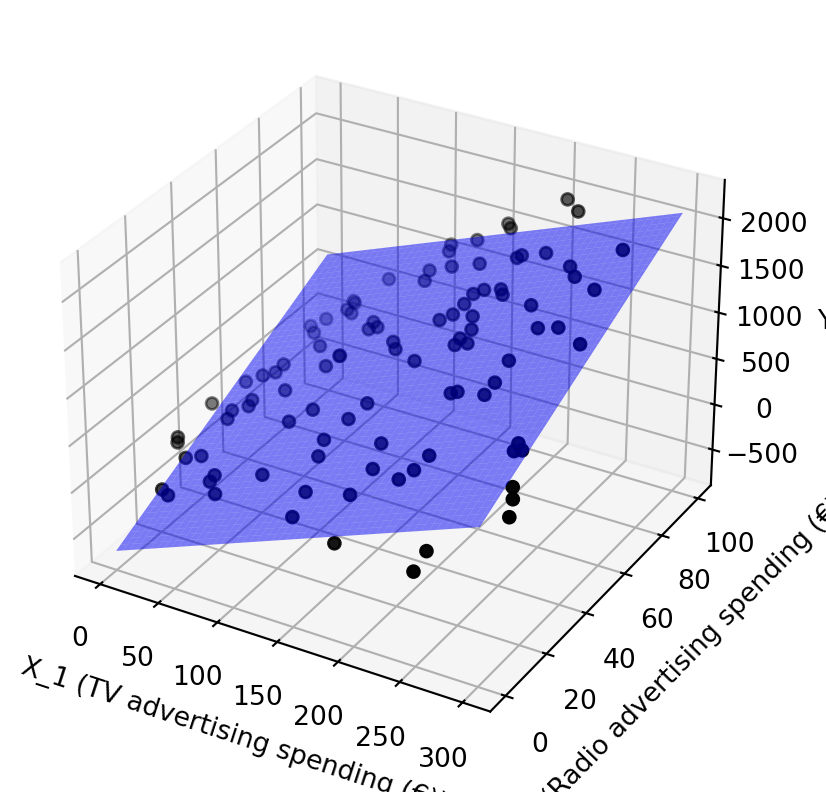
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Wir können das Modell visualisieren, indem wir dreidimensionale Daten plotten. Wir lassen \(x_3\) weg, da es den geringsten Einfluss auf die abhängige Variable zu haben scheint.

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

# Plot the data
ax.scatter(X_sample[0], X_sample[1], Y_sample, color='black')

# Plot the regression plane
x1 = np.linspace(0, 300, 100)
x2 = np.linspace(0, 100, 100)
X1, X2 = np.meshgrid(x1, x2)
Y_pred = model_sm.params[0] + model_sm.params[1] * X1 + model_sm.params[2] * X2 + model_sm.params[3] * 0    
ax.plot_surface(X1, X2, Y_pred, alpha=0.5, color='blue')
ax.set_xlabel('X_1 (TV advertising spending (€))')
ax.set_ylabel('X_2 (Radio advertising spending (€))')
ax.set_zlabel('Y (Sales)')
ax.set_zlabel('Y')

plt.show()
/tmp/ipykernel_3497/1194729202.py:14: FutureWarning:

Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`

Das Modell ist linear und jede der drei Variablen hat einen positiven Einfluss auf die abhängige Variable. Das Modell kann wie folgt geschrieben werden:

\[ Y = -689.7 + 4.9 X_1 + 13.3 X_2 + 0.6 X_3, \]

oder noch klarer:

\[ \text{sales} = 689.7 \text{units} + 4.9 \frac{\text{units}}{Euro} \times \text{TV advertising spending} + 13.3 \frac{\text{units}}{Euro} \times \text{Radio advertising spending} + 0.6 \frac{\text{units}}{Euro} \times \text{Newspaper advertising spending}. \]

Dieses lineare Modell eigent sich ausgezeichnet für eine Interpretation des Daten.

Korrelation und Kausalität

Streng genommen, zeigt sich immer nur die Korrelation zwischen den Variablen. Es ist nicht möglich, aus einer Korrelation auf eine Kausalität zu schließen. Es könnte auch sein, dass ganz andere Effekte die Verkäufe beeinflussen, die wir nicht gemessen haben.

Wichtig ist auch, dass wir unsere Interpretation der Welt durch unser Modell nicht verabsolutieren. Es ist immer nur eine Näherung und kann nie die Realität vollständig abbilden. Wenn wir unser Model wörtlich nehmen, könnten wir uns in die Irre führen. Stellen, wir uns vor, die Firma stellt die Werbeausgaben für Zeitungswerbung ein. Dann würde unser Modell den folgenden Absatz vorhersagen:

\[ \text{sales} = - 689.7 \text{units} \]

Ein negativer Absatz ist offensichtlich in der Realität nicht zu erwarten. Entsprechend haben wir den Grenzen unseres Modells erreicht. Die reale Welt lässt sich nur in bestimmten Grenzen durch das lineare Modell abbilden.

All Models are wrong, some are useful!
— George E. P. Box,

8.1 Abbildung nicht-linearer Zusammenhänge mit Linearen Modellen

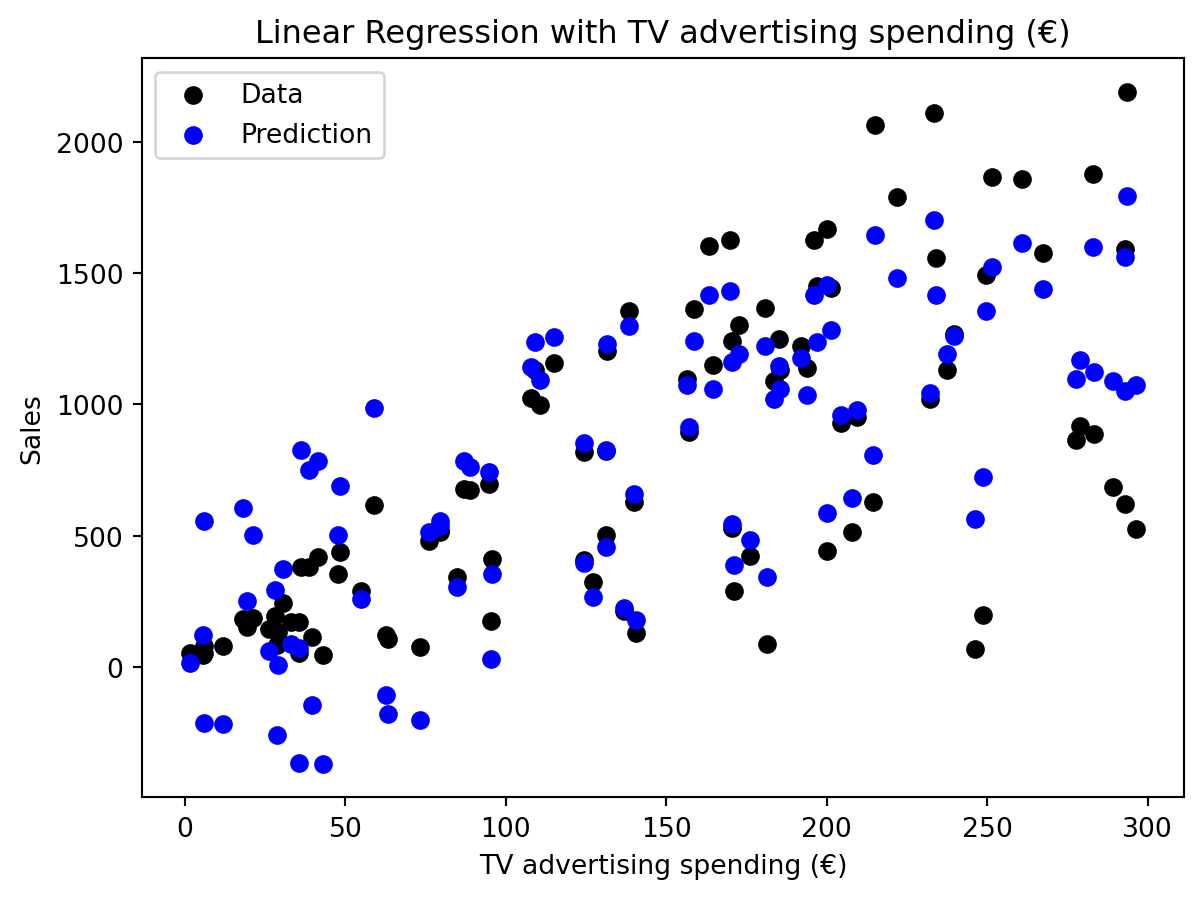
In der Praxis hört man oft, dass sich lineare Modelle nur für lineare Zusammenhänge eignen. Das ist nicht ganz richtig. Lineare Modelle können auch nicht-lineare Zusammenhänge abbilden. Zunächst vergegenwärtigen wir uns nochmal was passiert, wenn wir die Vorhersage unseres Modells nur in Abhängigkeit von einer Variablen betrachten. Jeder schwarze Punkt in (fig:regression-linear-advanced-linear-regression?) zeigt die beobachtete Absatzmenge zu einem Zeitpunkt in Abhängigkeit von den Werbeausgaben für TV-Spots. Der blaue Punkt zeigt die Vorhersage unseres Modells, in das Modell geht natürlich auch die Werbeausgaben für Radio- und Zeitungswerbung ein. Deswegen liegen die blauen Punkte nicht auf einer Linie, obwohl wir ein lineares Modell verwenden.

from sklearn.linear_model import LinearRegression

# Prediction for TV advertising spending
X = X_sample[0]
plt.scatter(X, Y_sample, color='black')
Y_pred = model_sm.params[0] + model_sm.params[1] * X_1 + model_sm.params[2] * X_2 + model_sm.params[3] * X_3
plt.scatter(X_1, Y_pred, color='blue')
plt.xlabel("TV advertising spending (€)")
plt.ylabel("Sales")
plt.title("Linear Regression with TV advertising spending (€)")
# Add legend
plt.legend(["Data", "Prediction"])
plt.show()
/tmp/ipykernel_3497/1829400649.py:6: FutureWarning:

Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`

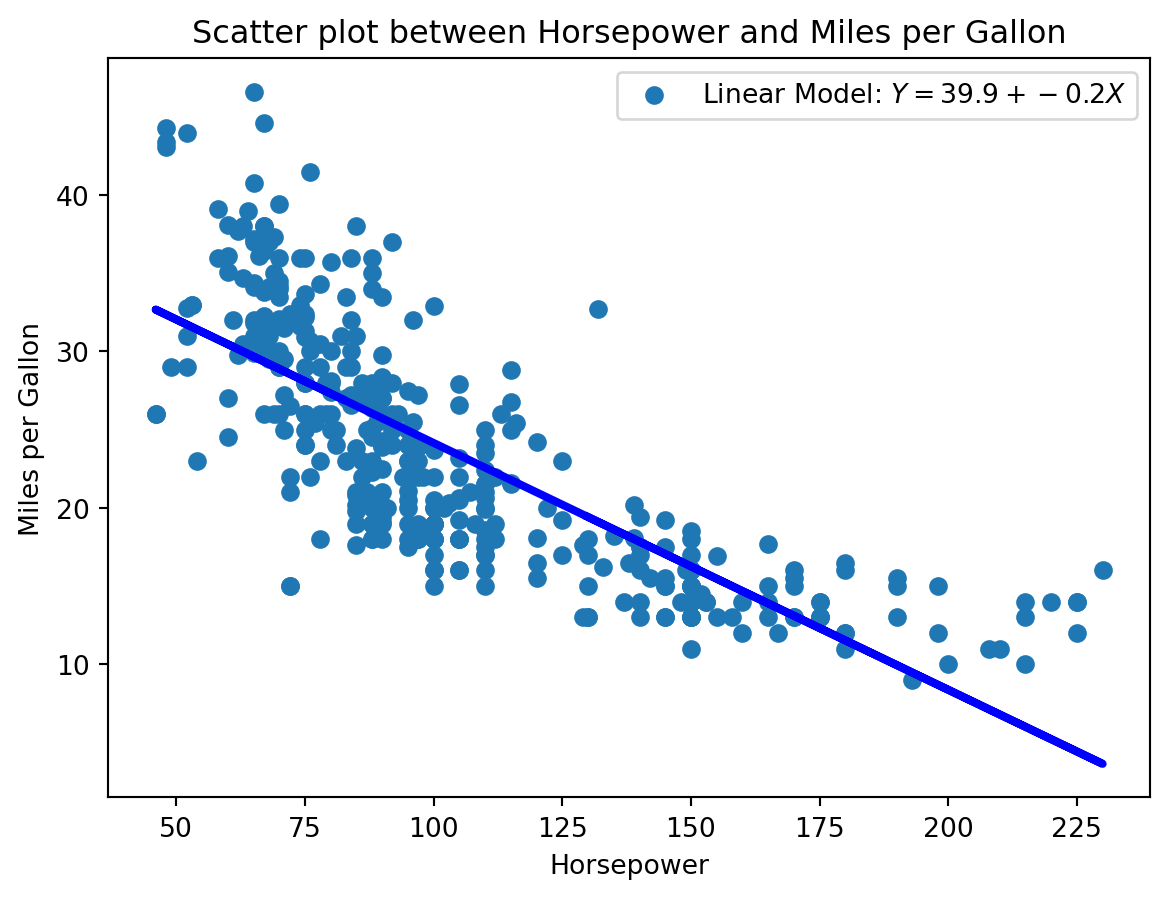
Lineare Regression für die drei unabhängigen Variablen als Plot für eine

Lineare Regression für die drei unabhängigen Variablen als Plot für eine

Manchmal begegnen wir Zusammenhängen, die ganz klar nicht linear sind, beispielsweise der zwischen Verbrauch in Meilen pro Gallone und der Leistung eines Autos. Offensichtlich sinkt der Verbrauch nicht linear mit der Leistung:

import pandas as pd
from sklearn.linear_model import LinearRegression

df = pd.read_csv(r"../_assets/regression/Auto_Data_Set_963_49.csv")

# linear model

model = LinearRegression()
model.fit(df[["horsepower"]], df["mpg"])
Y_pred = model.predict(df[["horsepower"]])


# Scatter plot between mpg und horsepower
plt.scatter(df["horsepower"], df["mpg"])
plt.plot(df["horsepower"], Y_pred, color='blue', linewidth=3)
plt.xlabel("Horsepower")
plt.ylabel("Miles per Gallon")
plt.title("Scatter plot between Horsepower and Miles per Gallon")
# Legend with parameters
plt.legend([f"Linear Model: $Y = {model.intercept_:.1f} + {model.coef_[0]:.1f}X$"])
# Add RSS

plt.show()

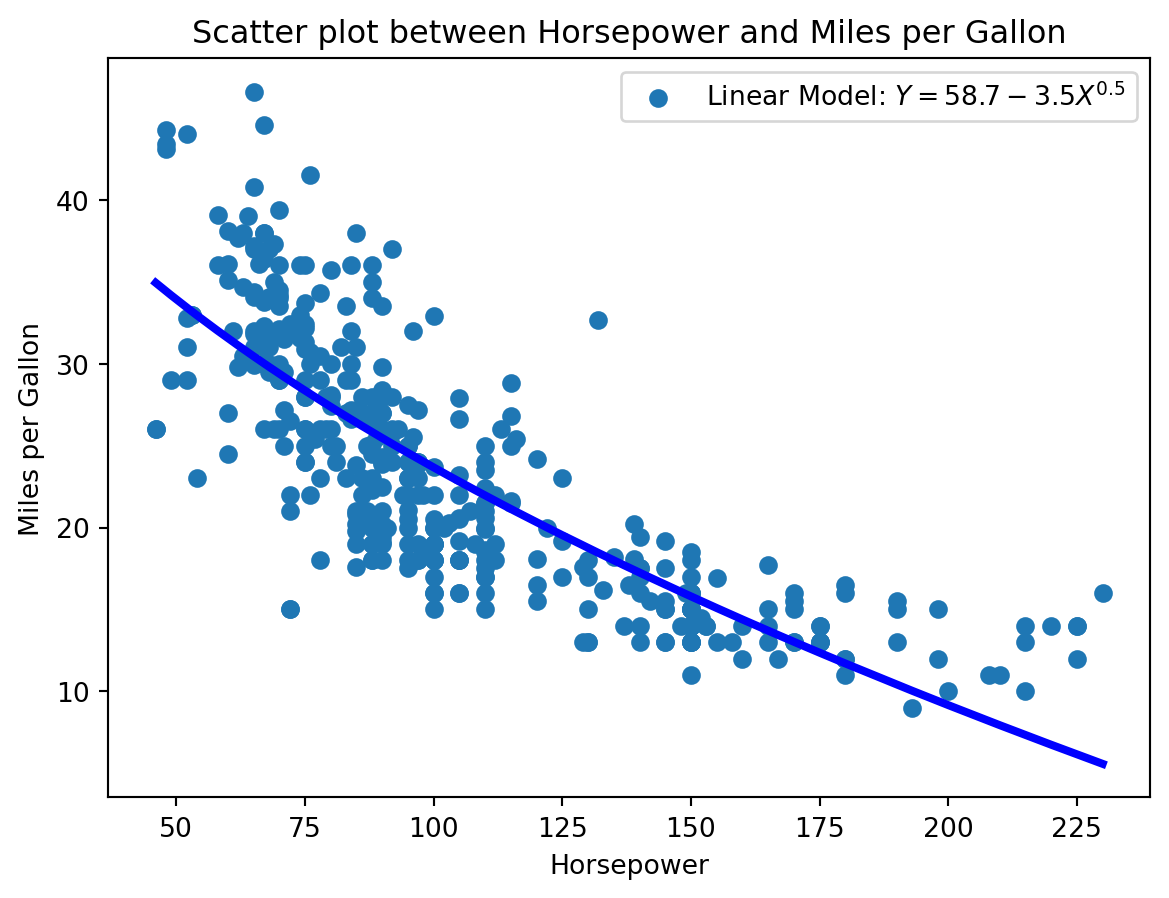
Eine Lösung ist die Transformation der unabhängigen Variablen. In unserem Beispiel könnten wir die Quadratwurzel der Leistung verwenden. Das Modell wird dann wie folgt aussehen:

\[ \text{mpg} = \beta_0 + \beta_1 \sqrt{\text{horsepower}} + \epsilon \]

# Transformation of the independent variable
df["sqrt_horsepower"] = np.sqrt(df["horsepower"])

# linear model
model = LinearRegression()
model.fit(df[["sqrt_horsepower"]], df["mpg"])

# Sort before plotting
df = df.sort_values(by="horsepower")

Y_pred = model.predict(df[["sqrt_horsepower"]])

# Scatter plot between mpg und horsepower
plt.scatter(df["horsepower"], df["mpg"])
plt.plot(df["horsepower"], Y_pred, color='blue', linewidth=3)
plt.xlabel("Horsepower")
plt.ylabel("Miles per Gallon")
plt.title("Scatter plot between Horsepower and Miles per Gallon")
# Legend with parameters
plt.legend([f"Linear Model: $Y = {model.intercept_:.1f} {model.coef_[0]:.1f}X^{{0.5}}$"])
plt.show()

Lineare Regression für mit transformierten unabhängigen Variablen

Lineare Regression für mit transformierten unabhängigen Variablen
Feature Engineering

Die Transformation der unabhängigen Variablen wird auch als Feature Engineering bezeichnet. Feature Engineering ist ein wichtiger Schritt in der Modellierung, um die Leistungsfähigkeit von Modellen zu verbessern.

8.2 Umgang mit Kategorischen Variablen

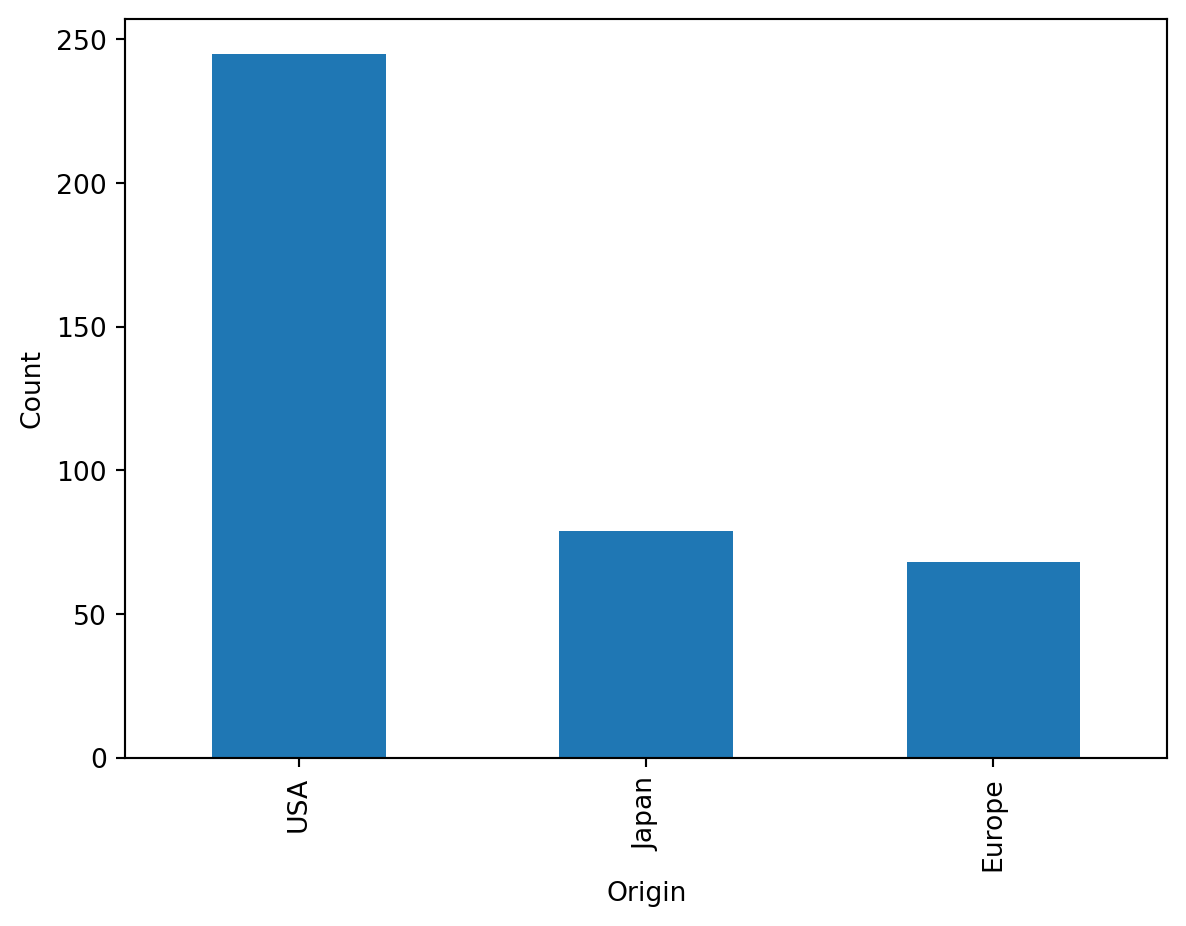
Bisher haben wir nur numerische Variablen betrachtet. In der Praxis haben wir es aber oft mit kategorischen Variablen zu tun. Kategorische Variablen sind Variablen, die eine endliche Anzahl von Kategorien haben. Beispiele sind Geschlecht, Region oder Produkttyp. Beispielsweise wird im Car-Data-Set die Herkunft der Autos erfasst.

df["origin"] = df["origin"].map({1: "USA", 2: "Europe", 3: "Japan"})
df["origin"].value_counts().plot(kind='bar')
plt.xlabel("Origin")
plt.ylabel("Count")
Text(0, 0.5, 'Count')

Nun wollen wir untersuchen, ob wir die Herkunft der Autos verwenden können, um den Verbrauch vorherzusagemn. Wie immer starten wir mit einer explorativen Analyse.

import seaborn as sns

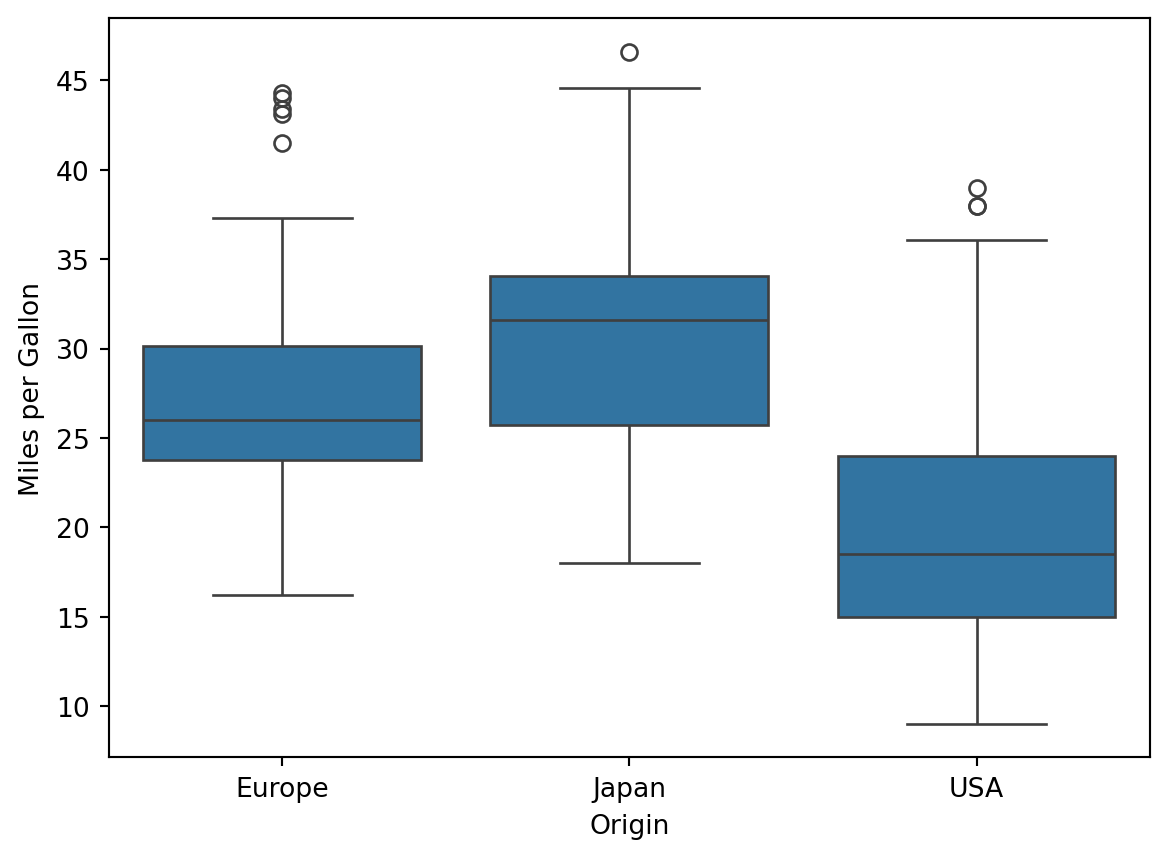
sns.boxplot(x="origin", y="mpg", data=df)
plt.xlabel("Origin")
plt.ylabel("Miles per Gallon")
Text(0, 0.5, 'Miles per Gallon')

Offensichtlich gibt es hier einen Zusammenhang. Wir wollen unser Modell von vorhin erweiten, um es weiter zu verbessern. Um kategoriale Variablen in einer Linearen Regression zu Berücksichtigen gibt es zwei Möglichkeiten.

8.2.1 Dummy-Variablen

Dummy-Variablen ermöglichen die Einbindung kategorischer Variablen in lineare Regressionsmodelle, indem sie jede Kategorie (außer einer Referenzkategorie) durch eine binäre Variable (0 oder 1) darstellen. Für eine Variable mit \(k\) Kategorien benötigt man \(k-1\) Dummy-Variablen, da die Referenzkategorie durch das Fehlen aller Dummy-Variablen kodiert wird. Dies vermeidet Mehrkollinearität, da die Kategorien sonst linear abhängig wären.

Beispiel: Wir verwenden die Spalte „origin“ (USA, Europe, Japan) aus dem Auto-Datensatz und erstellen Dummy-Variablen mit USA als Referenzkategorie.

import pandas as pd

# Lade den Datensatz
df = pd.read_csv(r"../_assets/regression/Auto_Data_Set_963_49.csv")
df["origin"] = df["origin"].map({1: "USA", 2: "Europe", 3: "Japan"})

# Erstelle Dummy-Variablen
dummy_df = pd.get_dummies(df["origin"], prefix="origin", drop_first=True)

# Füge die Dummy-Variablen zum DataFrame hinzu
df_with_dummies = pd.concat([df[["mpg", "horsepower"]], dummy_df], axis=1)

# Zeige die ersten Zeilen des DataFrames
print(df_with_dummies.head())
    mpg  horsepower  origin_Japan  origin_USA
0  18.0         130         False        True
1  15.0         165         False        True
2  18.0         150         False        True
3  16.0         150         False        True
4  17.0         140         False        True

Ergebnis: Der DataFrame enthält nun zwei neue Spalten: origin_Japan und origin_USA. Wenn origin_Japan = 1, ist das Auto aus Japan; wenn origin_USA = 1, aus den USA; wenn beide 0 sind, aus Europa (Referenzkategorie).

Interpretation: Diese Dummy-Variablen können in eine lineare Regression eingebunden werden, um den Einfluss der Herkunft auf den Verbrauch (mpg) zu modellieren. Der Koeffizient von origin_Japan gibt den Unterschied im durchschnittlichen Verbrauch zwischen europäischen und japanischen Autos an, bei konstanten anderen Variablen.

8.2.2 One-Hot-Encoding

One-Hot-Encoding kodiert jede Kategorie einer kategorischen Variable durch eine eigene binäre Spalte, was \(k\) Spalten für \(k\) Kategorien ergibt. Im Gegensatz zu Dummy-Variablen wird keine Referenzkategorie weggelassen, was in linearen Regressionen zu Mehrkollinearität führen kann, wenn der Intercept im Modell enthalten ist. In solchen Fällen wird oft eine Spalte entfernt oder der Intercept ausgeschlossen.

Beispiel: Wir erstellen ein One-Hot-Encoding für die Spalte „origin“ (USA, Europe, Japan) im Auto-Datensatz.

import pandas as pd

# Lade den Datensatz
df = pd.read_csv(r"../_assets/regression/Auto_Data_Set_963_49.csv")
df["origin"] = df["origin"].map({1: "USA", 2: "Europe", 3: "Japan"})

# Erstelle One-Hot-Encoding
one_hot_df  =  pd.get_dummies(df["origin"], prefix="origin", drop_first=False)
# Füge die One-Hot-Encoding-Spalten zum DataFrame hinzu
df_with_one_hot = pd.concat([df[["mpg", "horsepower"]], one_hot_df], axis=1)

# Zeige die ersten Zeilen des DataFrames
print(df_with_one_hot.head())
    mpg  horsepower  origin_Europe  origin_Japan  origin_USA
0  18.0         130          False         False        True
1  15.0         165          False         False        True
2  18.0         150          False         False        True
3  16.0         150          False         False        True
4  17.0         140          False         False        True

Ergebnis: Der DataFrame enthält drei neue Spalten: origin_USA, origin_Europe und origin_Japan. Jede Spalte zeigt an, ob ein Auto der jeweiligen Kategorie angehört (1) oder nicht (0).

Interpretation: In einer linearen Regression mit diesen One-Hot-kodierten Variablen und einem Intercept würde eine der Spalten (z. B. origin_USA) entfernt werden müssen, um Mehrkollinearität zu vermeiden. Alternativ kann das Modell ohne Intercept geschätzt werden, wobei jede Spalte den durchschnittlichen Verbrauch der jeweiligen Kategorie repräsentiert.

8.2.3 Modell nur mit Kategorischen Variablen

Ein Regressionsmodell, das ausschließlich kategorische Variablen verwendet, schätzt die Mittelwerte der abhängigen Variable für jede Kategorie. Für die Herkunft (USA, Europe, Japan) modelliert das Modell den durchschnittlichen Kraftstoffverbrauch (mpg) pro Land. Der Intercept entspricht dem durchschnittlichen Verbrauch der Referenzkategorie, während die Koeffizienten der Dummy-Variablen die Differenz im Verbrauch der anderen Kategorien im Vergleich zur Referenzkategorie angeben.

Beispiel: Wir erstellen ein Modell, das den Verbrauch (mpg) basierend auf der Herkunft vorhersagt, mit USA als Referenzkategorie.

import pandas as pd
import statsmodels.api as sm

# Lade den Datensatz
df = pd.read_csv(r"../_assets/regression/Auto_Data_Set_963_49.csv")
df["origin"] = df["origin"].map({1: "USA", 2: "Europe", 3: "Japan"})

# Erstelle Dummy-Variablen (USA als Referenzkategorie)
X = pd.get_dummies(df["origin"], prefix="origin", drop_first=True)
X = sm.add_constant(X)  # Füge Intercept hinzu

# Wandle Booleans in numerische Werte um
X = X.astype(int)

print(X.head())

# Fitte das Modell
model = sm.OLS(df["mpg"], X).fit()

# Zeige die Zusammenfassung
print(model.summary())
   const  origin_Japan  origin_USA
0      1             0           1
1      1             0           1
2      1             0           1
3      1             0           1
4      1             0           1
                            OLS Regression Results                            
==============================================================================
Dep. Variable:                    mpg   R-squared:                       0.332
Model:                            OLS   Adj. R-squared:                  0.328
Method:                 Least Squares   F-statistic:                     96.60
Date:                Tue, 24 Jun 2025   Prob (F-statistic):           8.67e-35
Time:                        07:09:56   Log-Likelihood:                -1282.2
No. Observations:                 392   AIC:                             2570.
Df Residuals:                     389   BIC:                             2582.
Df Model:                           2                                         
Covariance Type:            nonrobust                                         
================================================================================
                   coef    std err          t      P>|t|      [0.025      0.975]
--------------------------------------------------------------------------------
const           27.6029      0.776     35.587      0.000      26.078      29.128
origin_Japan     2.8477      1.058      2.691      0.007       0.767       4.928
origin_USA      -7.5695      0.877     -8.634      0.000      -9.293      -5.846
==============================================================================
Omnibus:                       26.330   Durbin-Watson:                   0.763
Prob(Omnibus):                  0.000   Jarque-Bera (JB):               30.217
Skew:                           0.679   Prob(JB):                     2.74e-07
Kurtosis:                       3.066   Cond. No.                         5.42
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Ergebnis und Interpretation:

  • Intercept: Der Intercept repräsentiert den durchschnittlichen Verbrauch (mpg) von Autos aus den USA (Referenzkategorie). Zum Beispiel, wenn der Intercept 27.6 ist, bedeutet dies, dass europäische Autos im Durchschnitt 27.6 Meilen pro Gallone erreichen.
  • Koeffizienten:
    • Der Koeffizient für origin_Japan gibt die Differenz im durchschnittlichen Verbrauch zwischen europäischen und japanischen Autos an. Ein positiver Koeffizient (z. B. 2.8) bedeutet, dass japanische Autos im Durchschnitt 2.8 Meilen pro Gallone sparsamer sind als europäische Autos.
    • Der Koeffizient für origin_USA interpretiert sich analog.
  • Modellqualität: Der \(R^2\)-Wert gibt an, wie viel der Varianz im Verbrauch durch die Herkunft erklärt wird. Ein niedriger \(R^2\) deutet darauf hin, dass andere Faktoren (z. B. Leistung) ebenfalls wichtig sind.

Dieses Modell ist einfach zu interpretieren, da es nur die Mittelwerte pro Kategorie vergleicht, ähnlich einer ANOVA oder einem T-Test.

8.2.4 Modell mit allen Variablen

Ein Modell, das numerische und kategorische Variablen kombiniert, nutzt alle verfügbaren Prädiktoren, um die abhängige Variable zu modellieren. Dies führt oft zu einer höheren Erklärungskraft (z. B. höherem \(R^2\)), da mehr Informationen berücksichtigt werden. Die Interpretation wird jedoch komplexer, da die Koeffizienten unter der Annahme interpretiert werden, dass alle anderen Variablen konstant sind.

Beispiel: Wir modellieren den Verbrauch (mpg) basierend auf der Leistung (horsepower), deren Quadratwurzel (für nicht-lineare Effekte) und der Herkunft (als Dummy-Variablen, USA als Referenzkategorie).

import pandas as pd
import statsmodels.api as sm
import numpy as np

# Lade den Datensatz
df = pd.read_csv(r"../_assets/regression/Auto_Data_Set_963_49.csv")
df["origin"] = df["origin"].map({1: "USA", 2: "Europe", 3: "Japan"})

# Erstelle transformierte Variable
df["sqrt_horsepower"] = np.sqrt(df["horsepower"])

# Erstelle Dummy-Variablen
X = pd.get_dummies(df["origin"], prefix="origin", drop_first=True)

# Füge numerische Variablen hinzu
X["horsepower"] = df["horsepower"]
X["sqrt_horsepower"] = df["sqrt_horsepower"]

# Füge Intercept hinzu
X = sm.add_constant(X)

# Wandle Booleans in numerische Werte um
X = X.astype(float)

# Fitte das Modell
model = sm.OLS(df["mpg"], X).fit()

# Zeige die Zusammenfassung
print(model.summary())
                            OLS Regression Results                            
==============================================================================
Dep. Variable:                    mpg   R-squared:                       0.719
Model:                            OLS   Adj. R-squared:                  0.716
Method:                 Least Squares   F-statistic:                     247.8
Date:                Tue, 24 Jun 2025   Prob (F-statistic):          2.51e-105
Time:                        07:09:56   Log-Likelihood:                -1112.2
No. Observations:                 392   AIC:                             2234.
Df Residuals:                     387   BIC:                             2254.
Df Model:                           4                                         
Covariance Type:            nonrobust                                         
===================================================================================
                      coef    std err          t      P>|t|      [0.025      0.975]
-----------------------------------------------------------------------------------
const              95.6047      6.489     14.734      0.000      82.847     108.362
origin_Japan        2.8432      0.688      4.134      0.000       1.491       4.195
origin_USA         -1.2807      0.632     -2.026      0.043      -2.523      -0.038
horsepower          0.3650      0.057      6.456      0.000       0.254       0.476
sqrt_horsepower   -10.9359      1.232     -8.875      0.000     -13.359      -8.513
==============================================================================
Omnibus:                       17.102   Durbin-Watson:                   1.198
Prob(Omnibus):                  0.000   Jarque-Bera (JB):               26.045
Skew:                           0.324   Prob(JB):                     2.21e-06
Kurtosis:                       4.084   Cond. No.                     3.52e+03
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 3.52e+03. This might indicate that there are
strong multicollinearity or other numerical problems.

Ergebnis und Interpretation:

  • Modellgüte: Der \(R^2\)-Wert ist höher als in Modellen mit nur numerischen oder nur kategorischen Variablen, da das Modell mehr Informationen nutzt. Zum Beispiel könnte \(R^2 = 0.75\) bedeuten, dass 75 % der Varianz im Verbrauch erklärt werden.
  • Koeffizienten:
    • Der Koeffizient für horsepower und sqrt_horsepower gibt den Einfluss der Leistung auf den Verbrauch an, unter Berücksichtigung der nicht-linearen Beziehung.
  • Interpretationsschwierigkeit: Die Koeffizienten sind schwerer zu interpretieren, da sie unter der Annahme konstanter anderer Variablen gelten. Zum Beispiel könnte der Einfluss von horsepower durch die Quadratwurzel-Transformation komplexer sein.
  • Vorsicht: Ein komplexeres Modell kann zu Überanpassung führen, insbesondere bei kleinen Datensätzen, und die Interpretation kann für praktische Entscheidungen unpraktisch werden.

Dieses Modell ist leistungsfähiger, aber die Interpretation erfordert ein tieferes Verständnis der Zusammenhänge und der Modellannahmen.

8.3 Matrixschreibweise der linearen Regression

Die lineare Regression schätzt die abhängige Variable \(y\) als lineare Kombination der Prädiktoren \(x_1, x_2, \dots, x_p\) plus eines Intercepts. Mathematisch wird dies als Matrixmultiplikation dargestellt, was die Berechnung effizient macht, insbesondere bei vielen Beobachtungen und Prädiktoren. Formel Die lineare Regression für \(n\) Beobachtungen und \(p\) Prädiktoren (inkl. Intercept) lautet: \[\mathbf{y} = \mathbf{X} \boldsymbol{\beta} + \boldsymbol{\epsilon}\]

  • \(\mathbf{y}\): Vektor der abhängigen Variable (\(n \times 1\)).
  • \(\mathbf{X}\): Designmatrix (\(n \times (p+1)\)), enthält eine Spalte für den Intercept (konstante 1) und die Prädiktoren.
  • \(\boldsymbol{\beta}\): Koeffizientenvektor (\(((p+1) \times 1)\)), enthält Intercept und Koeffizienten der Prädiktoren.
  • \(\boldsymbol{\epsilon}\): Fehlervektor (\(n \times 1\)).

Die vorhergesagten Werte sind: \[\hat{\mathbf{y}} = \mathbf{X} \boldsymbol{\beta}\] Matrixdarstellung mit Variablen Für die OLS-Regression mit mpg als abhängige Variable und Prädiktoren origin_Japan, origin_USA, horsepower, sqrt_horsepower lautet die Matrixform:

\[ \begin{bmatrix} \hat{y}_1 \\ \hat{y}_2 \\ \vdots \\ \hat{y}_n \end{bmatrix} = \begin{bmatrix} 1 & x_{1,\text{Japan}} & x_{1,\text{USA}} & x_{1,\text{hp}} & x_{1,\text{sqrt\_hp}} \\ 1 & x_{2,\text{Japan}} & x_{2,\text{USA}} & x_{2,\text{hp}} & x_{2,\text{sqrt\_hp}} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 1 & x_{n,\text{Japan}} & x_{n,\text{USA}} & x_{n,\text{hp}} & x_{n,\text{sqrt\_hp}} \end{bmatrix} \begin{bmatrix} \beta_0 \\ \beta_1 \\ \beta_2 \\ \beta_3 \\ \beta_4 \end{bmatrix} \]

  • \(\beta_0\): Intercept (const).
  • \(\beta_1, \beta_2\): Koeffizienten für origin_Japan, origin_USA.
  • \(\beta_3, \beta_4\): Koeffizienten für horsepower, sqrt_horsepower.
  • \(x_{i,\text{Japan}}, x_{i,\text{USA}}\): Dummy-Variablen (0 oder 1).
  • \(x_{i,\text{hp}}, x_{i,\text{sqrt\_hp}}\): Werte für horsepower und dessen Quadratwurzel.

8.3.1 Konkretes Beispiel

Nehmen wir die Koeffizienten aus der OLS-Ausgabe:

  • \(\beta_0 = 95.6047\) (const)
  • \(\beta_1 = 2.8432\) (origin_Japan)
  • \(\beta_2 = -1.2807\) (origin_USA)
  • \(\beta_3 = 0.3650\) (horsepower)
  • \(\beta_4 = -10.9359\) (sqrt_horsepower)

Für drei Beobachtungen aus dem Datensatz (angenommen):

Beobachtung origin horsepower sqrt_horsepower
1 USA 130 \(\sqrt{130} \approx 11.40\)
2 Japan 88 \(\sqrt{88} \approx 9.38\)
3 Europe 100 \(\sqrt{100} = 10.00\)

Die Designmatrix \(\mathbf{X}\) für diese Beobachtungen ist:

\[ \mathbf{X} = \begin{bmatrix} 1 & 0 & 1 & 130 & 11.40 \\ 1 & 1 & 0 & 88 & 9.38 \\ 1 & 0 & 0 & 100 & 10.00 \\ \end{bmatrix} \]

Der Koeffizientenvektor ist:

\[ \boldsymbol{\beta} = \begin{bmatrix} 95.6047 \\ 2.8432 \\ -1.2807 \\ 0.3650 \\ -10.9359 \\ \end{bmatrix} \]

Die vorhergesagten Werte \(\hat{\mathbf{y}}\) berechnen sich durch \(\hat{\mathbf{y}} = \mathbf{X} \boldsymbol{\beta}\). Für Beobachtung 1 (USA):

\[ \begin{align*} \hat{y}_1 &= 95.6047 + 0 \cdot 2.8432 + 1 \cdot (-1.2807) + 130 \cdot 0.3650 + 11.40 \cdot (-10.9359) \\ &= 95.6047 - 1.2807 + 47.45 - 124.66 \\ &= 17.11 \end{align*} \]