7 Lineare Regression
Die lineare Regression ist ein statistisches Verfahren, das dazu verwendet wird, die Beziehung zwischen einer abhängigen Variable \(Y\) und einer oder mehreren unabhängigen Variablen \(X\) zu modellieren. Das Modell der linearen Regression kann als eine lineare Beziehung zwischen \(Y\) und \(X\) interpretiert werden, die durch die Gleichung
\[ Y = f(X, \theta) + \epsilon, \]
7.1 Linare Regression mit einer Variablen
Für den Fall, dass wird nur eine Variable \(X\) betrachten, wird die lineare Regression durch die Gleichung: \[ Y = \beta_0 + \beta_1 X + \epsilon \]
beschrieben wird. Hierbei sind \(\beta_0\) und \(\beta_1\) die Parameter \(\theta\) des Modells, die die Steigung und den Achsenabschnitt der Regressionsgeraden bestimmen, und \(\epsilon\) ist der Fehlerterm, der die Abweichung der beobachteten Werte von den vorhergesagten Werten beschreibt.
In diesem Fall haben wir einen einfachen Zusammenhang zwischen nur zwei Variablen \(X\) und \(Y\). In der Praxis kann die lineare Regression jedoch auch auf mehrere unabhängige Variablen erweitert werden, um komplexere Beziehungen zu modellieren.
Die lineare Regression ist ein Beispiel für ein überwachtes Lernverfahren, bei dem wir ein Modell auf Basis von gelabelten Trainingsdaten erstellen. Das bedeutet, dass wir sowohl die unabhängigen Variablen \(X\) als auch die abhängige Variable \(Y\) kennen und das Modell so anpassen, dass es die Beziehung zwischen \(X\) und \(Y\) möglichst gut abbildet. Wir können dabei überwachen wie gut sich das Modell mit verschiedenen Parametern an die Daten anpasst und das Modell so optimieren, dass es die besten Vorhersagen liefert.
Bei der linearen Regression handelt es sich um ein parametrisches Modell, bei dem wir eine bestimmte Form der Beziehung zwischen \(X\) und \(Y\) annehmen und die Parameter \(\theta\) des Modells so anpassen, dass es die Daten möglichst gut abbildet. Im Gegensatz dazu gibt es auch nicht-parametrische Modelle, bei denen keine spezifische Form der Beziehung angenommen wird und das Modell flexibler ist, aber auch mehr Daten benötigt, um zuverlässige Vorhersagen zu treffen (z.B. Neuronale Netze).
Es gibt grundlegend zwei Zielstellungen, die mit der linearen Regression, und auch vielen anderen Modellen, verfolgt werden können:
- Interpretation: Die Interpretation der Beziehung zwischen den Variablen \(X\) und \(Y\) steht im Vordergrund. Hierbei geht es darum, die Auswirkung der unabhängigen Variablen auf die abhängige Variable zu verstehen und zu erklären und ggf. Hypothesen zu testen.
- Prognose: Die Vorhersage von Werten der abhängigen Variablen \(Y\) auf Basis der unabhängigen Variablen \(X\) steht im Vordergrund. Hierbei geht es darum, die Genauigkeit der Vorhersagen zu maximieren und die Modellgüte zu optimieren.
Wichtig ist es, sich vor der Anwendung eines Modells klar zu machen, welches Ziel verfolgt wird.
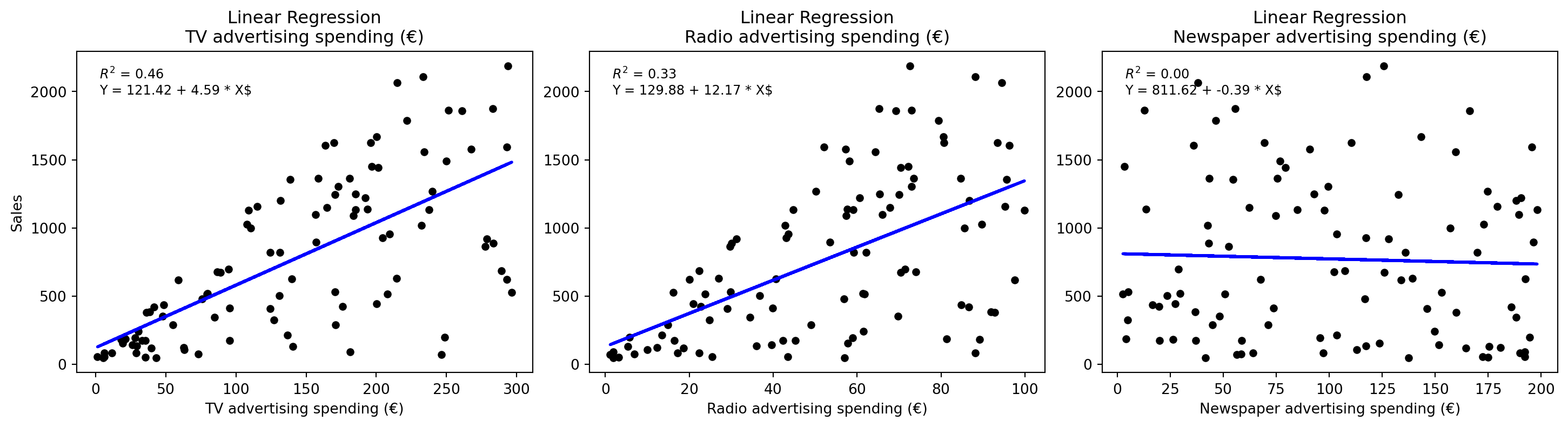
7.2 Beispiel: Vorhersage von Zeitungenverkäufen
- Interpretation:
- Gibt es einen Zusammenhang zwischen den Werbeausgaben und den Verkäufen?
- Wie stark ist der Zusammenhang?
- Welche Ausgaben haben den größten Einfluss auf die Verkäufe?
- Ist die Beziehung linear oder nicht-linear?
- Gibt es Synergieeffekte zwischen den verschiedenen Werbekanälen?
- Prognose:
- Wie gut können wir die Verkäufe vorhersagen, wenn wir die Werbeausgaben kennen?
- Wie genau sind unsere Vorhersagen?
Wenn wir das lineare Modell aufstellen könnte, wir das folgendermaßen aussehen:
\[ Y ≈ β_0 + β_1 \cdot X_1, \]
bzw. in unserem Beispiel:
\[ \text{sales} ≈ β_0 + β_1 \cdot \text{TV} \]
Die Parameter \(β_0\) und \(β_1\) haben dabei bestimmt Bedeutungen:
- \(β_0\) … intercept oder y-Achsenabschnitt
- \(β_1\) … slope oder Steigung
Als nächstes müssen wir einen Weg finden die Parameter \(β_0\) und \(β_1\) zu schätzen. Dafür gibt es verschiedene Methoden. Die Klassische Methode ist die Methode der kleinsten Quadrate (OLS). Diese Methode minimiert die Summe der quadrierten Abweichungen zwischen den beobachteten Werten und den vorhergesagten Werten.
\[Y ≈ \hat{β}_0 + \hat{β}_1 \cdot X_1\]
7.3 Methode der kleinsten Quadrate (OLS)
Die Methode der kleinsten Quadrate (OLS) ist ein Verfahren zur Schätzung der Parameter eines linearen Regressionsmodells, das die Summe der quadrierten Abweichungen zwischen den beobachteten Werten und den vorhergesagten Werten minimiert.
Als erstes definieren wir den Fehler \(\epsilon_i\) für jeden Datenpunkt \(i\) als die Differenz zwischen dem beobachteten Wert \(y_i\) und dem vorhergesagten Wert \(\hat{y}_i\):
\[ \epsilon_i = y_i - \hat{y}_i. \]
Die Methode der kleinsten Quadrate zielt darauf ab, die Summe der quadrierten Fehler zu minimieren, d.h. die Summe der quadrierten Abweichungen zwischen den beobachteten Werten und den vorhergesagten Werten:
\[ \text{RSS} = \sum_{i=1}^{n} \epsilon_i^2 = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2. \]
Auf Englisch wird die Summe als Residual Sum of Squares (RSS) bezeichnet. Die Methode der kleinsten Quadrate sucht nun die Parameter \(\hat{\beta}_0\) und \(\hat{\beta}_1\), die die Summe der quadrierten Fehler minimieren:
\[ \hat{\beta}_0, \hat{\beta}_1 = \text{argmin}_{\beta_0, \beta_1} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2. \]
Die Methode der kleinsten Quadrate kann auch als Optimierungsproblem formuliert werden, bei dem wir eine Kostenfunktion (Cost Function) minimieren, die die Summe der quadrierten Fehler zwischen den beobachteten und den vorhergesagten Werten beschreibt. Die Kostenfunktion ist in diesem Fall die Residual Sum of Squares (RSS), die wir minimieren, um die besten Parameter für das Modell zu finden. Kostenfunktionen hängen in der Regel von Modell, den Daten und den Parametern ab und dienen dazu, die Güte des Modells zu bewerten und zu optimieren. Da wir meist ein festes Modell und Daten haben und nur die Parameter anpassen, können wir die Kostenfunktion als Funktion der Parameter betrachten, die wir minimieren wollen. Ein eng verwandtes Konzept ist die Verlustfunktion (Loss Function) oder Accuracy Measures, die in der Regel den Fehler zwischen den beobachteten und den vorhergesagten Werten beschreiben Die Kostenfunktion ist in der Regel eine Summe der Verlustfunktionen über alle Datenpunkte.
Die Methode der kleinsten Quadrate (Ordinary Least Squares, OLS) wird verwendet, um die Parameter einer linearen Regression zu schätzen. Ziel ist es, die Gerade
\[ y_i = \beta_0 + \beta_1 x_i + \varepsilon_i, \]
wobei \(y_i\) die beobachtete abhängige Variable, \(\beta_0\) der Achsenabschnitt, \(\beta_1\) die Steigung und \(\varepsilon_i\) der Fehlerterm ist, so zu bestimmen, dass die Summe der quadrierten Fehler (Residual Sum of Squares, RSS) minimiert wird:
\[ RSS = \sum_{i=1}^{n} \left(y_i - \hat{y}i\right)^2 = \sum{i=1}^{n} \left(y_i - \beta_0 - \beta_1 x_i\right)^2. \]
Hierbei ist \(\hat{y}_i = \beta_0 + \beta_1 x_i\) die geschätzte abhängige Variable. Im Folgenden leiten wir die optimalen Parameter \(\hat{\beta}_0\) und \(\hat{\beta}_1\) Schritt für Schritt her.
- Berechnung der Mittelwerte
Für die Herleitung der Parameter ist es hilfreich, zunächst die Mittelwerte der unabhängigen Variable \(x\) und der abhängigen Variable \(y\) zu berechnen:
\[ \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i, \quad \bar{y} = \frac{1}{n} \sum_{i=1}^{n} y_i. \]
Diese Mittelwerte werden später verwendet, um die Formeln für \(\hat{\beta}_0\) und \(\hat{\beta}_1\) zu vereinfachen.
- Minimierung der Kostenfunktion nach \(\hat{\beta}_1\)
Um den optimalen Wert für \(\hat{\beta}_1\) zu finden, minimieren wir die Kostenfunktion \(RSS\) durch Ableiten nach \(\beta_1\) und Setzen der Ableitung gleich null:
\[ \frac{\partial RSS}{\partial \beta_1} = 0. \]
Die Kostenfunktion lautet:
\[ RSS = \sum_{i=1}^{n} \left(y_i - \beta_0 - \beta_1 x_i\right)^2. \]
Die partielle Ableitung nach \(\beta_1\) erfordert die Anwendung der Kettenregel.
Die Kettenregel ist ein zentrales Werkzeug in der Optimierung, da die Kostenfunktion \(RSS\) eine zusammengesetzte Funktion ist. Für eine Funktion \(f(g(x)) = [g(x)]^2\), wobei \(g(x) = y_i - \beta_0 - \beta_1 x_i\), lautet die Ableitung:
\[ \frac{d}{dx} [g(x)]^2 = 2 \cdot g(x) \cdot g'(x). \]
In unserem Fall ist \(g(\beta_1) = y_i - \beta_0 - \beta_1 x_i\), und die Ableitung von \(g\) nach \(\beta_1\) ergibt:
\[ \frac{\partial}{\partial \beta_1} (y_i - \beta_0 - \beta_1 x_i) = -x_i. \]
Somit wird die partielle Ableitung der Kostenfunktion:
\[ \frac{\partial RSS}{\partial \beta_1} = \sum_{i=1}^{n} \frac{\partial}{\partial \beta_1} \left(y_i - \beta_0 - \beta_1 x_i\right)^2 = \sum_{i=1}^{n} 2 \left(y_i - \beta_0 - \beta_1 x_i\right) \cdot (-x_i). \]
Dies vereinfacht sich zu:
\[ \frac{\partial RSS}{\partial \beta_1} = -2 \sum_{i=1}^{n} x_i \left(y_i - \beta_0 - \beta_1 x_i\right). \]
Setzen wir die Ableitung gleich null:
\[ -2 \sum_{i=1}^{n} x_i \left(y_i - \beta_0 - \beta_1 x_i\right) = 0. \]
Dividieren durch \(-2\) ergibt:
\[ \sum_{i=1}^{n} x_i \left(y_i - \beta_0 - \beta_1 x_i\right) = 0. \]
Ausklammern und Umformen führt zu:
\[ \sum_{i=1}^{n} x_i y_i - \beta_0 \sum_{i=1}^{n} x_i - \beta_1 \sum_{i=1}^{n} x_i^2 = 0. \]
Mit \(\sum_{i=1}^{n} x_i = n \bar{x}\) wird dies:
\[ \sum_{i=1}^{n} x_i y_i - \beta_0 n \bar{x} - \beta_1 \sum_{i=1}^{n} x_i^2 = 0. \]
- Minimierung der Kostenfunktion nach \(\hat{\beta}_0\)
Analog leiten wir die Kostenfunktion nach \(\beta_0\) ab:
\[ \frac{\partial RSS}{\partial \beta_0} = 0. \]
Die partielle Ableitung lautet:
\[ \frac{\partial RSS}{\partial \beta_0} = \sum_{i=1}^{n} \frac{\partial}{\partial \beta_0} \left(y_i - \beta_0 - \beta_1 x_i\right)^2 = -2 \sum_{i=1}^{n} \left(y_i - \beta_0 - \beta_1 x_i\right). \]
Setzen wir gleich null:
\[ -2 \sum_{i=1}^{n} \left(y_i - \beta_0 - \beta_1 x_i\right) = 0. \]
Dividieren durch \(-2\) ergibt:
\[ \sum_{i=1}^{n} \left(y_i - \beta_0 - \beta_1 x_i\right) = 0. \]
Dies führt zu:
\[ \sum_{i=1}^{n} y_i - \beta_0 \sum_{i=1}^{n} 1 - \beta_1 \sum_{i=1}^{n} x_i = 0. \]
Da \(\sum_{i=1}^{n} 1 = n\) und \(\sum_{i=1}^{n} x_i = n \bar{x}\), folgt:
\[ \sum_{i=1}^{n} y_i - n \beta_0 - \beta_1 n \bar{x} = 0. \]
Umformen nach \(\beta_0\) ergibt:
\[ n \beta_0 = \sum_{i=1}^{n} y_i - \beta_1 n \bar{x}. \]
Teilen durch \(n\) liefert:
\[ \beta_0 = \frac{1}{n} \sum_{i=1}^{n} y_i - \beta_1 \frac{1}{n} \sum_{i=1}^{n} x_i = \bar{y} - \beta_1 \bar{x}. \]
- Berechnung von \(\hat{\beta}_1\)
Um \(\hat{\beta}_1\) zu bestimmen, lösen wir die Gleichung aus Schritt 2 weiter auf. Wir verwenden die Formel für \(\hat{\beta}_1\), die sich aus der Minimierung ergibt. Eine alternative und intuitivere Darstellung ist:
\[ \hat{\beta}1 = \frac{\sum{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n} (x_i - \bar{x})^2}. \]
Diese Formel entspricht der Kovarianz von \(x\) und \(y\) geteilt durch die Varianz von \(x\). Die Kovarianz misst, wie stark \(x\) und \(y\) gemeinsam variieren, während die Varianz die Streuung von \(x\) beschreibt.
- Berechnung von \(\hat{\beta}_0\)
Setzen wir \(\hat{\beta}_1\) in die Gleichung für \(\beta_0\) ein:
\[ \hat{\beta}_0 = \bar{y} - \hat{\beta}_1 \bar{x}. \]
Dies stellt sicher, dass die Regressionsgerade durch den Mittelpunkt der Daten \((\bar{x}, \bar{y})\) verläuft.
- Ergebnis
Die geschätzte Regressionsgerade lautet:
\[ \hat{y} = \hat{\beta}_0 + \hat{\beta}_1 x. \]
Mit den berechneten Werten für \(\hat{\beta}_0\) und \(\hat{\beta}_1\) ist die OLS-Schätzung der Parameter abgeschlossen. Diese Parameter minimieren die Summe der quadrierten Fehler und liefern das beste lineare Modell für die gegebenen Daten.
7.4 Beispiel: Lineare Regression mit einer Variablen
Wir simulieren einen Datensatz mit einer linearen Beziehung zwischen \(X\) (€ ausgegeben für TV-Werbung) und \(Y\) (Verkäufe von Zeitungen). In diesem Fall kennen wir den Zufalls-Prozess, der die Daten generiert hat, und können daher die wahren Parameter des Modells bestimmen. Die Variable \(X\) ist gleichmäßig zwischen 0 und 300 verteilt, und \(Y\) wird durch die Gleichung \[ Y = 7 + 0.05 \cdot X + \epsilon \]
generiert, wobei \(\epsilon\) ein normalverteilter Fehler mit einer Standardabweichung von \(5\) ist.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# Simulate population data
np.random.seed(0)
X = 300 * np.random.rand(100, 1)
Y = 7 + 0.05 * X + 5 * np.random.randn(100, 1)
# Simulate sample data
sample_size = 100
idx = np.random.choice(100, sample_size, replace=False)
X_sample = X[idx]
Y_sample = Y[idx]
# Store data in a tidy dataframe
data = pd.DataFrame({"X (TV advertising spending (€))": X_sample.flatten(), "Y (Sales)": Y_sample.flatten()})
print(data.head()) X (TV advertising spending (€)) Y (Sales)
0 246.297969 14.750787
1 140.595360 22.596482
2 62.663027 6.953921
3 172.783949 21.579346
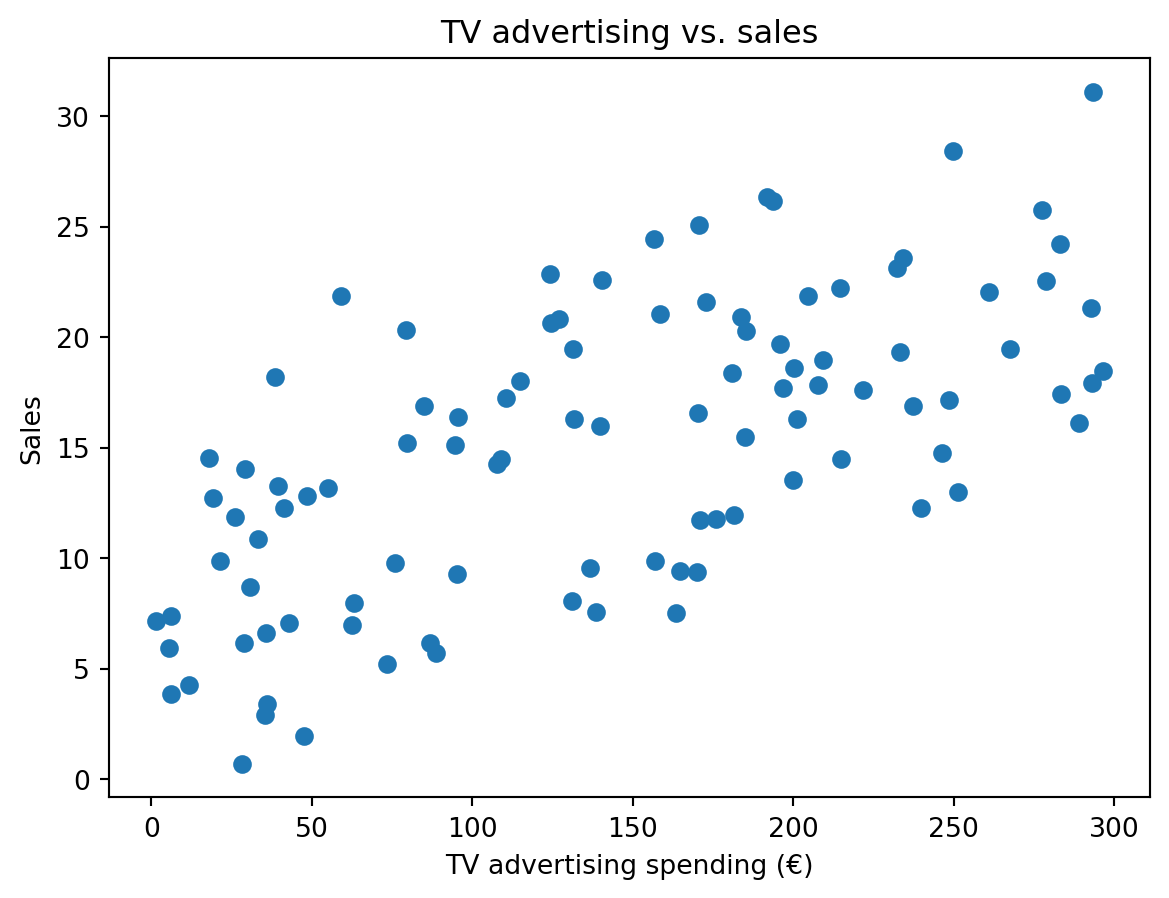
4 19.244249 12.709316# Plot data
plt.scatter(X, Y)
plt.xlabel("TV advertising spending (€)")
plt.ylabel("Sales")
plt.title("TV advertising vs. sales")
plt.show()Nun können wir unsere Formel für die OLS-Schätzung der Parameter \(\beta_0\) und \(\beta_1\) anwenden:
# Calculate means
X_mean = np.mean(X_sample)
Y_mean = np.mean(Y_sample)
# Calculate slope
numerator = np.sum((X_sample - X_mean) * (Y_sample - Y_mean))
denominator = np.sum((X_sample - X_mean) ** 2)
beta_1 = numerator / denominator
# Calculate intercept
beta_0 = Y_mean - beta_1 * X_mean
print(f"Slope (beta_1): {beta_1}")
print(f"Intercept (beta_0): {beta_0}")Slope (beta_1): 0.04894891702336733
Intercept (beta_0): 8.110755387236143In der Zukunft werden wir stattdessen eines von zwei Paketen verwenden, die die OLS-Schätzung automatisch durchführen: statsmodels oder scikit-learn.
7.4.1 scikit-learn
scikit-learn ist eine der bekanntesten Bibliotheken für maschinelles Lernen in Python. Sie bietet eine Vielzahl von Algorithmen und Werkzeugen für die Modellierung und Analyse von Daten. Wir werden es später und im kommenden Semester noch ausführlich verwenden.
from sklearn.linear_model import LinearRegression
# Defines what kind of model we want to use
model = LinearRegression()
# Fits the model to the data
model.fit(X_sample, Y_sample)
# Get slope and intercept from the models coefficients
beta_1_sklearn = model.coef_[0][0]
beta_0_sklearn = model.intercept_[0]
print(f"Slope (beta_1): {beta_1_sklearn}")
print(f"Intercept (beta_0): {beta_0_sklearn}")Slope (beta_1): 0.04894891702336733
Intercept (beta_0): 8.1107553872361437.4.2 statsmodels
statsmodels ist eine Bibliothek für statistische Modellierung in Python. Sie bietet eine Vielzahl von statistischen Modellen und Tests, darunter auch die lineare Regression. Die Ausgabe von statsmodels ist oft detaillierter und enthält mehr statistische Informationen als die von scikit-learn.
import statsmodels.api as sm
# Fit linear regression model
X_sm = sm.add_constant(X_sample)
model_sm = sm.OLS(Y_sample, X_sm).fit()
# Get slope and intercept
print(model_sm.summary()) OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.419
Model: OLS Adj. R-squared: 0.413
Method: Least Squares F-statistic: 70.80
Date: Tue, 24 Jun 2025 Prob (F-statistic): 3.29e-13
Time: 07:09:50 Log-Likelihood: -302.46
No. Observations: 100 AIC: 608.9
Df Residuals: 98 BIC: 614.1
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 8.1108 0.966 8.392 0.000 6.193 10.029
x1 0.0489 0.006 8.414 0.000 0.037 0.060
==============================================================================
Omnibus: 11.746 Durbin-Watson: 2.121
Prob(Omnibus): 0.003 Jarque-Bera (JB): 4.097
Skew: 0.138 Prob(JB): 0.129
Kurtosis: 2.047 Cond. No. 319.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.Anstelle die Daten in einem Numpy-Array zu speichern, können wir auch ein Pandas DataFrame verwenden. Dies hat den Vorteil, dass wir die Spalten mit ihren Namen ansprechen können und so den Code besser lesbar machen. Zudem läss sich die lineare Regression auch mit Hilfe von Formel-Strings durchführen, die die Beziehung zwischen den Variablen angeben.
import statsmodels.formula.api as smf
# Create DataFrame
data = pd.DataFrame({"TV": X_sample.flatten(), "Sales": Y_sample.flatten()})
# Fit linear regression model using formula string
model_smf = smf.ols("Sales ~ TV", data=data).fit()Wenn wir die Ergebnisse der OLS-Schätzung betrachten, sehen wir einige Zusatzinformationen, die uns helfen, die Güte des Modells zu bewerten
7.4.2.1 Koeffizienten und deren Konfidenzintervalle
Wir können die geschätzen Koeffizienten (coef) \(\hat{\beta}_0\) und \(\hat{\beta}_1\) sowie deren Konfidenzintervalle [0.025 0.975] ablesen. Es wird davon ausgegangen, dass die Schätzer der Koeffizienten normalverteilt sind. Entsprechend sind die Konfidenzintervalle symmetrisch um den Schätzer und 95% der Werte liegen innerhalb von zwei Standardabweichung des Schätzers z.B:
\[ [CI_{0.025}^{\beta_0}, CI^{\beta_0}_{0.975}] = [8.1108 - 2 0.966 , 8.1108 + 2 0.966] = [6.193, 10.029] \]
7.4.2.2 Teststatistiken \(t\) und \(p\)-Werte
Eine weitere wichtige Frage ist, ob ein Koeffizient (Parameter) tatsächlich siginifikant von \(0\) verschiedenen ist. Im unserem konkreten Beispiel stellt sich die Fragen: Verändert sich der Umsatz, wenn wir mehr Geld in TV-Werbung investieren? Dies kann mit einem T-Test überprüft werden.
- \(H_0\): \(\beta_1 = 0\) (kein Effekt)
- \(H_1\): \(\beta_1 \neq 0\) (Effekt)
Die Teststatistik \(t\) (t) gibt an, wie viele Standardabweichungen der Schätzer \(\hat{\beta}_1\) vom Wert \(0\) entfernt ist. Ein hoher \(t\)-Wert deutet darauf hin, dass der Schätzer signifikant von \(0\) verschieden ist. Der \(p\)-Wert (P>|t|) gibt die Wahrscheinlichkeit an, dass der beobachtete Effekt auftritt, wenn die Nullhypothese wahr ist. Ein \(p\)-Wert kleiner als \(0.05\) wird oft als Hinweis darauf interpretiert, dass der Effekt signifikant ist.
Im Vorliegenden Fall können wir also die Nullhypothese, dass der Umsatz unabhängig von den Werbeausgaben ist mit hoher Konfidenz ablehnen.
7.4.2.3 Bestimmtheitsmaß \(R^2\)
Der das Bestimmtheitsmaß \(R^2\) gibt an, wie gut das Modell die beobachteten Daten erklärt. Er liegt zwischen \(0\) und \(1\) und gibt den Anteil der Varianz der abhängigen Variable \(Y\) an, der durch das Modell erklärt wird. Ein \(R^2\) von \(1\) bedeutet, dass das Modell alle Variationen in \(Y\) erklärt, während ein \(R^2\) von \(0\) bedeutet, dass das Modell keine Variationen erklärt. In unserem Fall beträgt \(R^2 = 0.41\), was darauf hindeutet, dass das Modell etwa \(41\%\) der Variationen in den Verkäufen erklärt.
Das Bestimmtheitsmaß \(R^2\) ist definiert als: \[ R^2 = \frac{TSS-RSS}{TSS} = 1- \frac{RSS}{TSS}, \]
wobei \(RSS\) die Residual Sum of Squares (siehe oben) und \(TSS\) die Total Sum of Squares ist. \(TSS\) ist die Summe der quadrierten Abweichungen der abhängigen Variable \(Y\) von ihrem Mittelwert \(\bar{y}\).
Die Varianz und TSS hängen eng miteinander zusammen:
\[ TSS = \sum_{i=1}^{n} (y_i - \bar{y})^2 = n \text{Var}(Y). \]
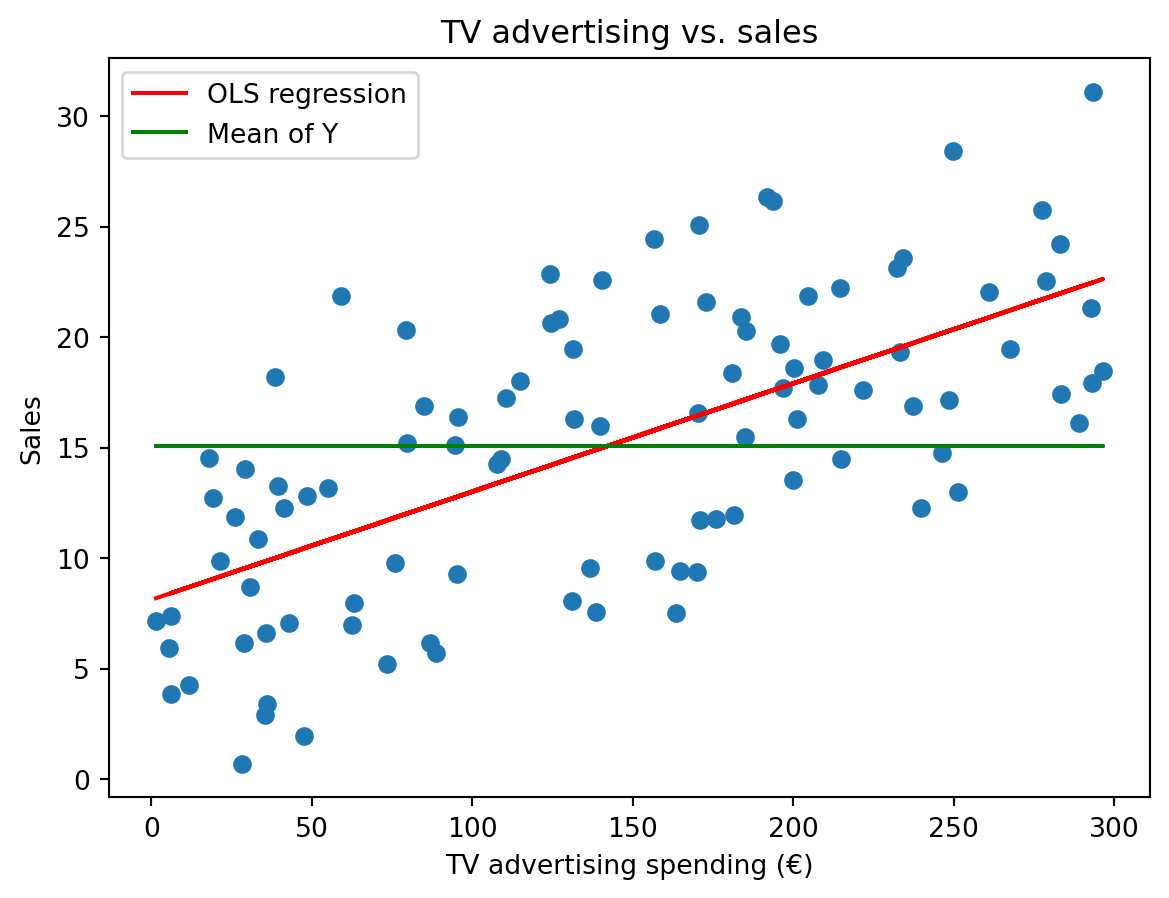
Intuitiv kann man sagen, R² gibt an, wie viel Prozent der Varianz der abhängigen Variable durch die unabhängigen Variablen erklärt wird, bzw. genauer: Wie veringern sich die Fehler, wenn man ein naives Mittel-Wert-Modells (\(f(x)=\bar{y}\)) durch das lineare Modell ersetzt.
# Plot data
plt.scatter(X, Y)
plt.plot(X, beta_0 + beta_1 * X, color="red", label="OLS regression")
plt.plot(X, np.mean(Y) * np.ones_like(X), color="green", label="Mean of Y")
plt.legend()
plt.xlabel("TV advertising spending (€)")
plt.ylabel("Sales")
plt.title("TV advertising vs. sales")
plt.show()- Ein hoher \(R^2\) bedeutet nicht unbedingt, dass das Modell gut ist. Ein Modell mit einem hohen \(R^2\) kann immer noch schlechte Vorhersagen machen, wenn es nicht gut generalisiert.
- Ein niedriger \(R^2\) bedeutet nicht unbedingt, dass das Modell schlecht ist. Ein Modell mit einem niedrigen \(R^2\) kann immer noch nützlich sein, wenn es die Beziehung zwischen den Variablen gut erklärt.
- \(R^2\) hängt von der Anzahl der Variablen im Modell ab. Ein Modell mit mehr Variablen wird tendenziell ein höheres \(R^2\) haben, auch wenn es nicht besser ist.
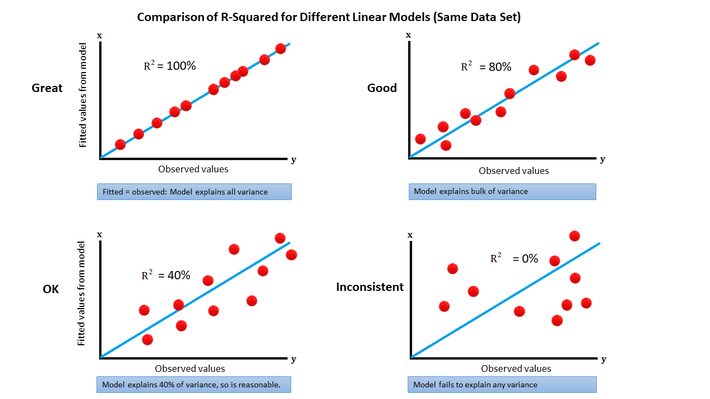
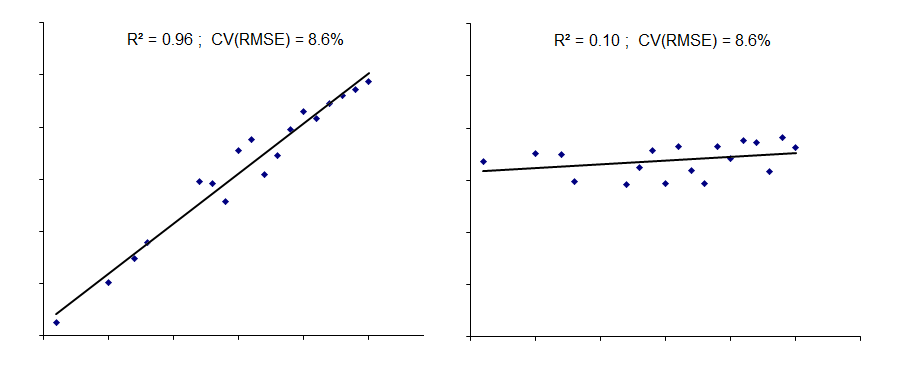
Die folgede Abbildung zeigt zudem verschiende Zusammenhänge und den \(R^2\) Wert für die jeweiligen Modelle.
Damit eine Lineare Regression sinnvoll ist und die Schätzung der Parameter gut funktioniert müssen einige Annahmen erfüllt sein:
- Lineare Beziehung: Die Beziehung zwischen den unabhängigen und abhängigen Variablen ist linear.
- Unabhängigkeit: Die Beobachtungen sind unabhängig voneinander.
- Homoskedastizität: Die Varianz der Fehler ist konstant.
- Normalverteilung: Die Fehler sind normalverteilt.
- Keine Multikollinearität: Die unabhängigen Variablen sind nicht stark miteinander korreliert
Nach Lehrbuch sind die Annahmen für die lineare Regression immer zu testen, wenn wir Sie für eine statische Analyse und Interpretation verwenden wollen. In der Praxis, vorallem im Fall von Vorhersagen, sind die Annahmen jedoch oft nicht erfüllt, und es ist wichtig, die Robustheit der Ergebnisse zu überprüfen und gegebenenfalls alternative Modelle oder Transformationen in Betracht zu ziehen.