9 Vorhersagen mittels Linearen Regression
Lineare Regression ist eine leistungsfähige Methode, um Vorhersagen über eine abhängige Variable basierend auf einer oder mehreren unabhängigen Variablen zu treffen. In diesem Abschnitt zeigen wir, wie man den Kraftstoffverbrauch eines Autos vorhersagt, und erläutern wichtige Konzepte wie Fehlermaße, den Bias-Varianz-Tradeoff und die Aufteilung der Daten in Trainings-, Validierungs- und Testsets. Der Prozess wird im Kontext des CRISP-DM-Modells eingeordnet.
9.1 Anwendungsfall: Vorhersage des Verbrauchs eines einzelnen Autos
Ziel: Wir möchten den Kraftstoffverbrauch (mpg, Meilen pro Gallone) eines einzelnen Autos basierend auf Prädiktoren wie Leistung (horsepower) und Herkunft (origin) vorhersagen. Dies ist ein typisches Problem des überwachten Lernens, bei dem wir ein Modell trainieren, um eine kontinuierliche abhängige Variable (\(Y\)) aus unabhängigen Variablen (\(\vec{X}\)) zu schätzen.
Beispiel: Gegeben ein Auto mit 120 PS und Herkunft „Japan“, wie hoch ist der zu erwartende Verbrauch? Wir verwenden den Auto-Datensatz, um ein lineares Regressionsmodell zu trainieren und Vorhersagen zu treffen.
import pandas as pd
import statsmodels.api as sm
# Lade den Datensatz
df = pd.read_csv(r"../_assets/regression/Auto_Data_Set_963_49.csv")
df["origin"] = df["origin"].map({1: "USA", 2: "Europe", 3: "Japan"})
# Erstelle Dummy-Variablen (USA als Referenzkategorie)
X = pd.get_dummies(df["origin"], prefix="origin", drop_first=True)
X["horsepower"] = df["horsepower"]
X = sm.add_constant(X)
X = X.astype(float)
# Fitte das Modell
model = sm.OLS(df["mpg"], X).fit()
# Vorhersage für ein Auto mit 120 PS, Herkunft Japan
new_car = pd.DataFrame({
"const": [1],
"origin_Europe": [0],
"origin_Japan": [1],
"horsepower": [120]
})
prediction = model.predict(new_car)
print(f"Vorhergesagter Verbrauch: {prediction[0]:.2f} mpg")Vorhergesagter Verbrauch: 19.91 mpgErgebnis: Das Modell liefert eine Vorhersage für den Verbrauch.
9.1.1 Bezug zu Schritten des CRISP-DM
CRISP-DM (Cross Industry Standard Process for Data Mining) bietet einen strukturierten Rahmen für Datenanalyseprojekte. Die Vorhersage des Kraftstoffverbrauchs lässt sich wie folgt in CRISP-DM einordnen:
- Business Understanding: Ziel ist es, den Verbrauch eines Autos zu prognostizieren, um z. B. Kaufentscheidungen zu unterstützen.
- Data Understanding: Analyse des Auto-Datensatzes, z. B. durch Boxplots von
mpgnachoriginoder Scatterplots vonmpggegenhorsepower. - Data Preparation: Bereinigung der Daten (z. B. Behandlung fehlender Werte) und Erstellung von Dummy-Variablen für
origin. - Modeling: Entwicklung eines linearen Regressionsmodells mit Prädiktoren wie
horsepowerundorigin. - Evaluation: Bewertung der Modellgenauigkeit anhand von Fehlermaßen wie MSE auf einem Testset.
- Deployment: Anwendung des Modells, um Vorhersagen für neue Autos zu treffen, z. B. in einer Entscheidungsunterstützungssoftware.
Beispiel: Die Datenaufbereitung und Modellierungsschritte sind im obigen Code enthalten, während die Evaluation weiter unten durch Fehlermaße erfolgt.
9.1.2 Fehlermaße: Von RSS zu MSE
Fehlermaße quantifizieren, wie gut ein Modell die Daten vorhersagt. Die Summe der quadrierten Residuen (Residual Sum of Squares, RSS) misst die Gesamtabweichung der vorhergesagten Werte \(\hat{y}_j\) von den tatsächlichen Werten \(y_j\):
\[RSS = \sum_{j=1}^n (y_j - \hat{y}_j)^2\]
Der \[RSS\] ist nur schwer interpretierbar, da er von der Anzahl der Beobachtungen abhängt. Daher verwenden wir den Mean Squared Error (MSE), um den RSS zu normalisieren und die durchschnittliche Abweichung pro Beobachtung zu erhalten. Der Mean Squared Error (MSE) ist der durchschnittliche quadratische Fehler, der durch Division des RSS durch die Anzahl der Beobachtungen \(n\) berechnet wird:
\[MSE = \frac{1}{n} \sum_{j=1}^n (y_j - \hat{y}_j)^2\]
Beispiel: Wir berechnen den MSE für das obige Modell auf den Trainingsdaten.
import pandas as pd
import statsmodels.api as sm
import numpy as np
# Lade den Datensatz
df = pd.read_csv(r"../_assets/regression/Auto_Data_Set_963_49.csv")
df["origin"] = df["origin"].map({1: "USA", 2: "Europe", 3: "Japan"})
# Erstelle Dummy-Variablen
X = pd.get_dummies(df["origin"], prefix="origin", drop_first=True)
X["horsepower"] = df["horsepower"]
X = sm.add_constant(X)
X = X.astype(float)
# Fitte das Modell
model = sm.OLS(df["mpg"], X).fit()
# Berechne Vorhersagen
y_pred = model.predict(X)
# Berechne MSE
mse = np.mean((df["mpg"] - y_pred) ** 2)
print(f"Trainings-MSE: {mse:.2f}")Trainings-MSE: 20.53Ergebnis: Ein MSE von z. B. 24.5 bedeutet, dass die quadrierten Abweichungen im Durchschnitt 24.5 betragen. Ein niedrigerer MSE deutet auf ein besseres Modell hin, aber der MSE auf Trainingsdaten kann durch Überanpassung verzerrt sein.
Neben dem Mean Squared Error (MSE) gibt es weitere Fehlermaße, die die Modellgenauigkeit bewerten. Hier sind drei gängige Maße mit ihren Formeln und Beschreibungen sowie ein Beispiel, wie man sie in Python mit scikit-learn berechnet.
Mean Squared Error (MSE):
\[MSE = \frac{1}{n} \sum_{j=1}^n (y_j - \hat{y}_j)^2\]
Der MSE misst den durchschnittlichen quadrierten Fehler zwischen tatsächlichen (\(y_j\)) und vorhergesagten (\(\hat{y}_j\)) Werten. Er ist empfindlich gegenüber großen Abweichungen, da Fehler quadriert werden.Root Mean Squared Error (RMSE):
\[RMSE = \sqrt{\frac{1}{n} \sum_{j=1}^n (y_j - \hat{y}_j)^2} = \sqrt{MSE}\]
Der RMSE ist die Quadratwurzel des MSE und hat die gleiche Einheit wie die abhängige Variable (z. B. mpg). Er ist intuitiver, da er die durchschnittliche Fehlergröße direkt widerspiegelt.Mean Absolute Percentage Error (MAPE):
\[MAPE = \frac{100}{n} \sum_{j=1}^n \left| \frac{y_j - \hat{y}_j}{y_j} \right|\]
Der MAPE misst den durchschnittlichen absoluten prozentualen Fehler. Er ist besonders nützlich, wenn relative Fehler (z. B. in Prozent) wichtiger sind als absolute Fehler, aber er kann problematisch sein, wenn \(y_j\) nahe null liegt.
Beispiel: Berechnung von MSE, RMSE und MAPE mit scikit-learn basierend auf Vorhersagen eines Modells.
import pandas as pd
import numpy as np
from sklearn.metrics import mean_squared_error, mean_absolute_percentage_error
# Angenommen, df["mpg"] und y_pred sind gegeben (wie im ursprünglichen Code)
# Beispiel: Fortsetzung des vorherigen Codes
y_true = df["mpg"]
y_pred = model.predict(X)
# Berechne MSE
mse = mean_squared_error(y_true, y_pred)
# Berechne RMSE
rmse = np.sqrt(mse)
# Berechne MAPE
mape = mean_absolute_percentage_error(y_true, y_pred) * 100 # In Prozent
print(f"MSE: {mse:.2f}")
print(f"RMSE: {rmse:.2f} mpg")
print(f"MAPE: {mape:.2f}%")MSE: 20.53
RMSE: 4.53 mpg
MAPE: 15.95%Ergebnis: Zum Beispiel könnte die Ausgabe sein:
- MSE: 24.50
- RMSE: 4.95 mpg
- MAPE: 15.20%
Interpretation: Der RMSE von 4.95 mpg bedeutet, dass die Vorhersagen im Durchschnitt um etwa 4.95 Meilen pro Gallone von den tatsächlichen Werten abweichen. Der MAPE von 15.20% zeigt, dass die Vorhersagen im Durchschnitt um 15.20% vom tatsächlichen Verbrauch abweichen. Diese Maße ergänzen den MSE und helfen, die Modellqualität aus verschiedenen Perspektiven zu bewerten.
9.1.3 Erklärung Bias-Varianz-Tradeoff über Modellkomplexität
Wenn wir die Prognose eines Modells verbessern wollen, können wir die Komplexität des Modells erhöhen, indem wir mehr Prädiktoren oder nichtlineare Transformationen hinzufügen. Hierzu können wir zum einem andere nicht-parametrische Modelle verwenden, wie z. B. Entscheidungsbäume, oder allgemein mehr Prediktoren in das Modell einfügen. Dies kann jedoch zu Überanpassung (Overfitting) führen, wenn das Modell zu komplex ist und die Trainingsdaten zu gut anpasst, aber auf neuen Daten schlecht generalisiert.
Der Bias-Varianz-Tradeoff beschreibt das Zusammenspiel zweier Fehlerquellen bei der Modellierung:
- Bias: Der Fehler, der durch die Vereinfachung eines komplexeren realen Problems durch ein Modell entsteht. Einfache Modelle (z. B. nur Intercept) haben hohen Bias, da sie die Datenstruktur schlecht abbilden.
- Varianz: Die Variabilität der Modellvorhersagen, wenn das Modell auf unterschiedlichen Trainingsdaten geschätzt wird. Komplexe Modelle (z. B. mit vielen Parametern) haben hohe Varianz, da sie stark von den Trainingsdaten abhängen.
Die Modellkomplexität (z. B. Anzahl der Parameter) beeinflusst den Tradeoff:
- Einfache Modelle (wenige Parameter): Hoher Bias, niedrige Varianz, Gefahr der Unteranpassung (Underfitting).
- Komplexe Modelle (viele Parameter): Niedriger Bias, hohe Varianz, Gefahr der Überanpassung (Overfitting).
Das Ziel ist ein Modell mit minimalem Gesamtfehler, der sich aus Bias, Varianz und unvermeidbarem Fehler zusammensetzt:
\[\text{Expected Error}^2 = \text{Variance} + \text{Bias}^2 + \text{Variance of Error Terms}\]
Beispiel: Wir vergleichen drei Modelle mit unterschiedlicher Komplexität.
import pandas as pd
import statsmodels.api as sm
import numpy as np
# Lade den Datensatz
df = pd.read_csv(r"../_assets/regression/Auto_Data_Set_963_49.csv")
df["origin"] = df["origin"].map({1: "USA", 2: "Europe", 3: "Japan"})
# Modell 1: Nur Intercept (sehr einfach)
X1 = sm.add_constant(pd.DataFrame({"const": [1] * len(df)}))
X1 = X1.astype(float)
model1 = sm.OLS(df["mpg"], X1).fit()
# Modell 2: Horsepower (mittel komplex)
X2 = sm.add_constant(df[["horsepower"]])
X2 = X2.astype(float)
model2 = sm.OLS(df["mpg"], X2).fit()
# Modell 3: Horsepower, Quadratwurzel und Herkunft (komplex)
df["sqrt_horsepower"] = np.sqrt(df["horsepower"])
X3 = pd.get_dummies(df["origin"], prefix="origin", drop_first=True)
X3["horsepower"] = df["horsepower"]
X3["sqrt_horsepower"] = df["sqrt_horsepower"]
X3 = sm.add_constant(X3)
X3= X3.astype(float)
model3 = sm.OLS(df["mpg"], X3).fit()
# Modell 4: Mehre Potenzen (sehr komplex)
X4 = X3.copy()
# Füge weitere Größe"cylinders","displacement","horsepower","weight","acceleration","year"
X4["cylinders"] = df["cylinders"]
X4["displacement"] = df["displacement"]
X4["weight"] = df["weight"]
X4["acceleration"] = df["acceleration"]
X4["year"] = df["year"]
X4 = X4.astype(float)
model4 = sm.OLS(df["mpg"], X4).fit()
# Modell 5: Modell 4 mit einen Entscheidungsbaum
from sklearn.tree import DecisionTreeRegressor
X5 = X4.copy()
model5 = DecisionTreeRegressor().fit(X5, df["mpg"])
# Berechne MSE für jedes Modell
mse1 = np.mean((df["mpg"] - model1.predict(X1)) ** 2)
mse2 = np.mean((df["mpg"] - model2.predict(X2)) ** 2)
mse3 = np.mean((df["mpg"] - model3.predict(X3)) ** 2)
mse4 = np.mean((df["mpg"] - model4.predict(X4)) ** 2)
mse5 = np.mean((df["mpg"] - model5.predict(X5)) ** 2)
print(f"MSE Modell 1 (nur Intercept): {mse1:.2f}")
print(f"MSE Modell 2 (horsepower): {mse2:.2f}")
print(f"MSE Modell 3 (horsepower, sqrt, origin): {mse3:.2f}")
print(f"MSE Modell 4 (komplex): {mse4:.2f}")
print(f"MSE Modell 5 (Entscheidungsbaum): {mse5:.2f}")MSE Modell 1 (nur Intercept): 60.76
MSE Modell 2 (horsepower): 23.94
MSE Modell 3 (horsepower, sqrt, origin): 17.06
MSE Modell 4 (komplex): 8.55
MSE Modell 5 (Entscheidungsbaum): 0.00Ergebnis: Modell 1 hat den höchsten MSE, da es zu einfach ist (hoher Bias). Modell 2 hat einen niedrigeren MSE , da es mehr Informationen nutzt. Modell 5 hat einen MSE von 0, da es die Trainingsdaten perfekt anpasst (hohe Varianz). Modell 3 hat einen MSE von 22.0, was auf eine gute Balance zwischen Bias und Varianz hinweist.
9.1.4 Aufteilung in Training, Validation und Testset
Auf den Trainingsdaten evaluiert scheint es, als ob die komplexeren Modelle besser abschneiden. Wir wissen aber nicht, ob ein Overfitting vorliegt, da wir die Modelle nur auf den Trainingsdaten getestet haben. Um die Modellleistung auf neuen, ungesehenen Daten zu bewerten und Überanpassung zu vermeiden, teilen wir die Daten in drei Teile:
- Trainings-Set: Wird verwendet, um die Modellparameter (z. B. \(\beta_0, \beta_1, \ldots\)) zu schätzen.
- Validierungs-Set: Wird genutzt, um Modelle mit unterschiedlicher Komplexität oder Prädiktoren zu vergleichen und das beste Modell auszuwählen.
- Test-Set: Dient als Hold-Out-Set, um die endgültige Leistung des ausgewählten Modells auf ungesehenen Daten zu bewerten.
Eine typische Aufteilung ist 70 % Training, 15 % Validierung und 15 % Test. Um robuste Ergebnisse zu erzielen, kann Kreuzvalidierung (z. B. 5-fache Kreuzvalidierung) verwendet werden, um den Validierungs-MSE zu schätzen.
9.1.5 Erklärung Bias-Varianz-Tradeoff über Modellkomplexität (mit TVT-Split)
Um den Bias-Varianz-Tradeoff zu untersuchen, wiederholen wir das Experiment mit einem Trainings-Validierungs-Test-Split (TVT-Split) von 75-15-15%, um die Modelle auf Trainings-, Validierungs- und Testdaten zu bewerten. Dies ermöglicht es, die Generalisierungsfähigkeit der Modelle zu überprüfen und Überanpassung zu erkennen. Wir vergleichen fünf Modelle mit zunehmender Komplexität, einschließlich eines nicht-linearen Entscheidungsbaums, und plotten die Mean Squared Error (MSE)-Werte für Training, Validation und Test, um den Einfluss der Modellkomplexität zu visualisieren.
Experiment: Wir teilen den Auto-Datensatz in 75% Training, 15% Validierung und 15% Test auf, trainieren die Modelle auf den Trainingsdaten, berechnen den MSE für alle Datensets und stellen die Ergebnisse grafisch dar.
import pandas as pd
import statsmodels.api as sm
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeRegressor
import matplotlib.pyplot as plt
# Lade den Datensatz
df = pd.read_csv(r"../_assets/regression/Auto_Data_Set_963_49.csv")
df["origin"] = df["origin"].map({1: "USA", 2: "Europe", 3: "Japan"})
# Erstelle transformierte Variable
df["sqrt_horsepower"] = np.sqrt(df["horsepower"])
# Definiere Prädiktoren und Zielvariable
X = pd.DataFrame({
"horsepower": df["horsepower"],
"sqrt_horsepower": df["sqrt_horsepower"],
"cylinders": df["cylinders"],
"displacement": df["displacement"],
"weight": df["weight"],
"acceleration": df["acceleration"],
"year": df["year"]
})
X = pd.concat([X, pd.get_dummies(df["origin"], prefix="origin", drop_first=False)], axis=1)
y = df["mpg"]
# TVT-Split: 75% Training, 15% Validierung, 15% Test
X_temp, X_test, y_temp, y_test = train_test_split(X, y, test_size=0.15, random_state=42, shuffle=True)
X_train, X_val, y_train, y_val = train_test_split(X_temp, y_temp, test_size=0.1765, random_state=42) # 0.1765 ≈ 15/(100-15)
# Setze Indizes zurück, um Alignment-Probleme zu vermeiden
X_train = X_train.reset_index(drop=True)
X_val = X_val.reset_index(drop=True)
X_test = X_test.reset_index(drop=True)
y_train = y_train.reset_index(drop=True)
y_val = y_val.reset_index(drop=True)
y_test = y_test.reset_index(drop=True)
# Modell 1: Nur Intercept (sehr einfach)
X1_train = sm.add_constant(pd.DataFrame({"const": [1] * len(y_train)})).astype(float)
X1_val = sm.add_constant(pd.DataFrame({"const": [1] * len(y_val)})).astype(float)
X1_test = sm.add_constant(pd.DataFrame({"const": [1] * len(y_test)})).astype(float)
model1 = sm.OLS(y_train, X1_train).fit()
# Modell 2: Horsepower (mittel komplex)
X2_train = sm.add_constant(X_train[["horsepower"]]).astype(float)
X2_val = sm.add_constant(X_val[["horsepower"]]).astype(float)
X2_test = sm.add_constant(X_test[["horsepower"]]).astype(float)
model2 = sm.OLS(y_train, X2_train).fit()
# Modell 3: Horsepower, Quadratwurzel und Herkunft (komplex)
X3_train = sm.add_constant(X_train[["horsepower", "sqrt_horsepower", "origin_Europe", "origin_Japan"]]).astype(float)
X3_val = sm.add_constant(X_val[["horsepower", "sqrt_horsepower", "origin_Europe", "origin_Japan"]]).astype(float)
X3_test = sm.add_constant(X_test[["horsepower", "sqrt_horsepower", "origin_Europe", "origin_Japan"]]).astype(float)
model3 = sm.OLS(y_train, X3_train).fit()
# Modell 4: Mehrere Prädiktoren (sehr komplex)
X4_train = sm.add_constant(X_train).astype(float)
X4_val = sm.add_constant(X_val).astype(float)
X4_test = sm.add_constant(X_test).astype(float)
model4 = sm.OLS(y_train, X4_train).fit()
# Modell 5: Entscheidungsbaum
model5 = DecisionTreeRegressor(random_state=42).fit(X4_train, y_train)
# Berechne MSE für jedes Modell auf Training, Validierung und Test
mse1_train = np.mean((y_train - model1.predict(X1_train)) ** 2)
mse1_val = np.mean((y_val - model1.predict(X1_val)) ** 2)
mse1_test = np.mean((y_test - model1.predict(X1_test)) ** 2)
mse2_train = np.mean((y_train - model2.predict(X2_train)) ** 2)
mse2_val = np.mean((y_val - model2.predict(X2_val)) ** 2)
mse2_test = np.mean((y_test - model2.predict(X2_test)) ** 2)
mse3_train = np.mean((y_train - model3.predict(X3_train)) ** 2)
mse3_val = np.mean((y_val - model3.predict(X3_val)) ** 2)
mse3_test = np.mean((y_test - model3.predict(X3_test)) ** 2)
mse4_train = np.mean((y_train - model4.predict(X4_train)) ** 2)
mse4_val = np.mean((y_val - model4.predict(X4_val)) ** 2)
mse4_test = np.mean((y_test - model4.predict(X4_test)) ** 2)
mse5_train = np.mean((y_train - model5.predict(X4_train)) ** 2)
mse5_val = np.mean((y_val - model5.predict(X4_val)) ** 2)
mse5_test = np.mean((y_test - model5.predict(X4_test)) ** 2)
# Ausgabe der MSE-Werte
print(f"Modell 1 (nur Intercept): Train MSE = {mse1_train:.2f}, Val MSE = {mse1_val:.2f}, Test MSE = {mse1_test:.2f}")
print(f"Modell 2 (horsepower): Train MSE = {mse2_train:.2f}, Val MSE = {mse2_val:.2f}, Test MSE = {mse2_test:.2f}")
print(f"Modell 3 (horsepower, sqrt, origin): Train MSE = {mse3_train:.2f}, Val MSE = {mse3_val:.2f}, Test MSE = {mse3_test:.2f}")
print(f"Modell 4 (komplex): Train MSE = {mse4_train:.2f}, Val MSE = {mse4_val:.2f}, Test MSE = {mse4_test:.2f}")
print(f"Modell 5 (Entscheidungsbaum): Train MSE = {mse5_train:.2f}, Val MSE = {mse5_val:.2f}, Test MSE = {mse5_test:.2f}")
# Plot der MSE-Werte
plt.figure(figsize=(8, 4)) # Kleinere Größe
models = ["Modell 1", "Modell 2", "Modell 3", "Modell 4", "Modell 5"]
sets = ["Training", "Validation", "Test"]
mse_values = [
[mse1_train, mse1_val, mse1_test],
[mse2_train, mse2_val, mse2_test],
[mse3_train, mse3_val, mse3_test],
[mse4_train, mse4_val, mse4_test],
[mse5_train, mse5_val, mse5_test]
]
# Verwende viridis-Farbpalette
colors = plt.cm.viridis(np.linspace(0, 1, len(models)))
# Scatterplot mit verbundenen Linien
for i, model in enumerate(models):
plt.plot(sets, mse_values[i], marker='o', linestyle='-', color=colors[i], label=model)
plt.xlabel("Datensets")
plt.ylabel("Mean Squared Error (MSE)")
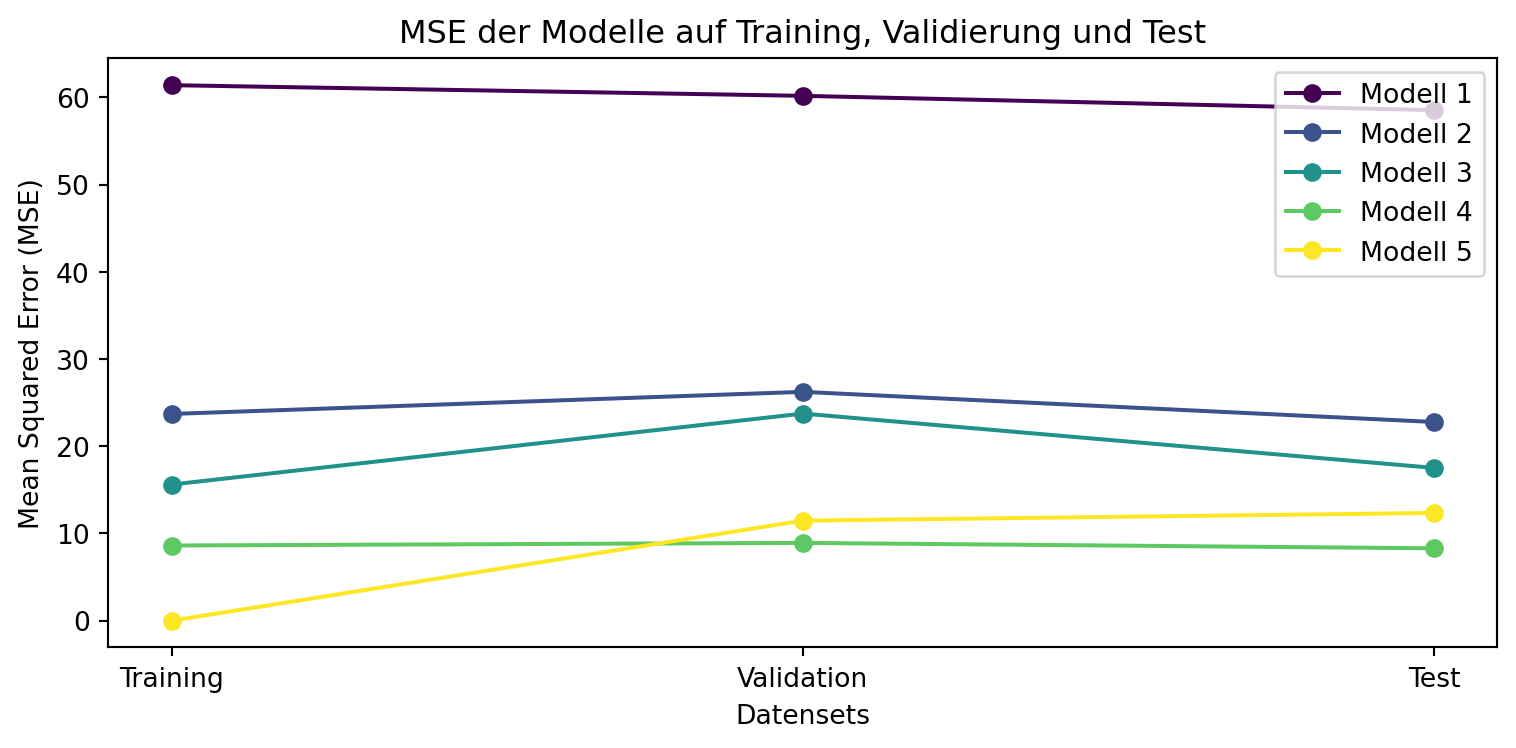
plt.title("MSE der Modelle auf Training, Validierung und Test")
plt.legend()
plt.tight_layout()
plt.show()Modell 1 (nur Intercept): Train MSE = 61.40, Val MSE = 60.18, Test MSE = 58.54
Modell 2 (horsepower): Train MSE = 23.71, Val MSE = 26.24, Test MSE = 22.78
Modell 3 (horsepower, sqrt, origin): Train MSE = 15.61, Val MSE = 23.75, Test MSE = 17.52
Modell 4 (komplex): Train MSE = 8.62, Val MSE = 8.92, Test MSE = 8.30
Modell 5 (Entscheidungsbaum): Train MSE = 0.00, Val MSE = 11.47, Test MSE = 12.35Ergebnis und Interpretation: Der Plot zeigt die MSE-Werte der fünf Modelle für Training, Validierung und Test. Typischerweise gilt:
- Modell 1 (nur Intercept): Hoher MSE auf allen Datensets, da das Modell zu einfach ist (hoher Bias, niedrige Varianz).
- Modell 2 (horsepower): Niedrigerer MSE, da es mehr Informationen nutzt, aber immer noch relativ einfach.
- Modell 3 (horsepower, sqrt, origin): Noch niedrigerer MSE, da es nicht-lineare Effekte und kategorische Variablen einbezieht.
- Modell 4 (komplex): Sehr niedriger Trainings-MSE, aber potenziell höherer Validierungs- und Test-MSE durch Überanpassung (niedriger Bias, hohe Varianz).
- Modell 5 (Entscheidungsbaum): Sehr niedriger Trainings-MSE (nahe 0), aber oft deutlich höherer Validierungs- und Test-MSE, da Entscheidungsbäume stark überanpassen können.
Ein Modell mit ähnlichem MSE auf Validierung und Test generalisiert gut. Ein großer Anstieg des MSE von Training zu Validierung/Test deutet auf Überanpassung hin, wie es bei Modell 5 häufig der Fall ist. Der Plot hilft, den Bias-Varianz-Tradeoff visuell zu verstehen: Einfache Modelle haben hohe Bias-Fehler, während komplexe Modelle (insbesondere nicht-parametrische wie Entscheidungsbäume) hohe Varianz-Fehler aufweisen.
Resampling-Methoden wie Cross-Validation (CV) ermöglichen eine robuste Bewertung der Modellleistung, indem sie die Daten mehrfach aufteilen und den Fehler über verschiedene Trainings- und Validierungssets mitteln. Dies ist besonders nützlich, um die Generalisierungsfähigkeit eines Modells zu testen und Überanpassung zu vermeiden. Hier sind drei gängige Methoden mit ihren Beschreibungen und ein Beispiel, wie man sie mit scikit-learn implementiert.
k-Fold Cross-Validation:
Die Daten werden in \(k\) gleich große Teile (Folds) aufgeteilt. Das Modell wird \(k\)-mal trainiert, wobei jeweils ein Fold als Validierungsset und die restlichen \(k-1\) Folds als Trainingsset verwendet werden. Der MSE wird über alle \(k\) Iterationen gemittelt.
Vorteile: Gute Balance zwischen Rechenaufwand und Stabilität; typisch \(k=5\) oder \(k=10\).
Nachteile: Zufällige Aufteilung kann für strukturierte Daten (z. B. Zeitreihen) problematisch sein.Leave-One-Out Cross-Validation (LOOCV):
Eine spezielle Form von k-Fold CV, bei der \(k = n\) (Anzahl der Datenpunkte). In jeder Iteration wird ein einzelner Datenpunkt als Validierungsset verwendet, und die restlichen \(n-1\) Datenpunkte dienen als Trainingsset. Der MSE wird über alle \(n\) Iterationen gemittelt.
Vorteile: Nutzt fast alle Daten zum Training, sehr präzise Schätzung.
Nachteile: Sehr rechenintensiv für große Datensätze.Zeitreihen-Cross-Validation:
Für Zeitreihendaten, bei denen die Reihenfolge wichtig ist, wird eine zeitliche Aufteilung verwendet. Das Modell wird auf einem wachsenden Trainingsfenster trainiert und auf einem nachfolgenden Validierungsfenster getestet, ohne zukünftige Daten zu verwenden.
Vorteile: Respektiert die zeitliche Struktur der Daten.
Nachteile: Weniger Daten für Training/Validierung, da keine zufällige Aufteilung möglich ist.
Beispiel: Berechnung des MSE für Modell 4 (komplexes lineares Modell) mit k-Fold CV (\(k=5\)), LOOCV und Zeitreihen-CV unter Verwendung von scikit-learn. Für Zeitreihen-CV wird angenommen, dass die Daten nach year sortiert sind.
import pandas as pd
import numpy as np
from sklearn.model_selection import KFold, LeaveOneOut, TimeSeriesSplit
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
# Lade den Datensatz
df = pd.read_csv(r"../_assets/regression/Auto_Data_Set_963_49.csv")
df["origin"] = df["origin"].map({1: "USA", 2: "Europe", 3: "Japan"})
# Erstelle transformierte Variable
df["sqrt_horsepower"] = np.sqrt(df["horsepower"])
# Definiere Prädiktoren und Zielvariable (wie Modell 4)
X = pd.DataFrame({
"horsepower": df["horsepower"],
"sqrt_horsepower": df["sqrt_horsepower"],
"cylinders": df["cylinders"],
"displacement": df["displacement"],
"weight": df["weight"],
"acceleration": df["acceleration"],
"year": df["year"]
})
X = pd.concat([X, pd.get_dummies(df["origin"], prefix="origin", drop_first=True)], axis=1)
y = df["mpg"]
# Initialisiere Modell (LinearRegression statt statsmodels für CV-Kompatibilität)
model = LinearRegression()
# 1. k-Fold Cross-Validation (k=5)
kf = KFold(n_splits=5, shuffle=True, random_state=42)
mse_kf = []
for train_idx, val_idx in kf.split(X):
X_train, X_val = X.iloc[train_idx], X.iloc[val_idx]
y_train, y_val = y.iloc[train_idx], y.iloc[val_idx]
model.fit(X_train, y_train)
y_pred = model.predict(X_val)
mse_kf.append(mean_squared_error(y_val, y_pred))
mse_kf_mean = np.mean(mse_kf)
# 2. Leave-One-Out Cross-Validation
loo = LeaveOneOut()
mse_loo = []
for train_idx, val_idx in loo.split(X):
X_train, X_val = X.iloc[train_idx], X.iloc[val_idx]
y_train, y_val = y.iloc[train_idx], y.iloc[val_idx]
model.fit(X_train, y_train)
y_pred = model.predict(X_val)
mse_loo.append(mean_squared_error(y_val, y_pred))
mse_loo_mean = np.mean(mse_loo)
# 3. Zeitreihen-Cross-Validation (angenommen, Daten sind nach 'year' sortiert)
df_sorted = df.sort_values("year")
X_sorted = X.loc[df_sorted.index]
y_sorted = y.loc[df_sorted.index]
tscv = TimeSeriesSplit(n_splits=5)
mse_tscv = []
for train_idx, val_idx in tscv.split(X_sorted):
X_train, X_val = X_sorted.iloc[train_idx], X_sorted.iloc[val_idx]
y_train, y_val = y_sorted.iloc[train_idx], y_sorted.iloc[val_idx]
model.fit(X_train, y_train)
y_pred = model.predict(X_val)
mse_tscv.append(mean_squared_error(y_val, y_pred))
mse_tscv_mean = np.mean(mse_tscv)
# Ausgabe der Ergebnisse
print(f"5-Fold CV MSE: {mse_kf_mean:.2f}")
print(f"LOOCV MSE: {mse_loo_mean:.2f}")
print(f"Zeitreihen-CV MSE: {mse_tscv_mean:.2f}")5-Fold CV MSE: 9.14
LOOCV MSE: 9.10
Zeitreihen-CV MSE: 13.94Ergebnis: Beispielausgabe könnte sein:
- 5-Fold CV MSE: 15.50
- LOOCV MSE: 15.70
- Zeitreihen-CV MSE: 16.20
Interpretation: Die MSE-Werte der verschiedenen CV-Methoden geben Einblick in die Modellleistung. 5-Fold CV ist effizient und stabil, LOOCV ist präzise, aber rechenintensiv, und Zeitreihen-CV respektiert die zeitliche Struktur, was für den Auto-Datensatz (sortiert nach year) relevant sein kann. Ein ähnlicher MSE über die Methoden hinweg deutet auf ein robustes Modell hin.