2.8.1 k-nearest Neighbors

Learning objectives

You will be able to

• describe the -Nearest Neighbors approach for classification and regression
• calculate Euclidean distance between two points in two dimensions
• perform standardization and normalization

One Dimension

Dimensions

Example: Species Classification

• prediction of the species based on beak length and depth

Task

• Calculate the distance between observation 1 and 2:

Distance Table for all Observations

• based on the beak length and depth

• What species of penguin is observation 6 based on its three nearest neighbors?

• What species of penguin is observation 6 based on its three nearest neighbors?
  • Number 5 (Adélie), 4 (Adélie) and 2 (Gentoo) are closest
  • Number 6 is probably an Adélie
  • We can use the majority vote to predict the species with a probability of 2/3

Problem 1: Curse of dimensionality

• everything works fine, if we have a limited number of predictors (features)
• the volume of the space increases so fast that the available data become sparse
  
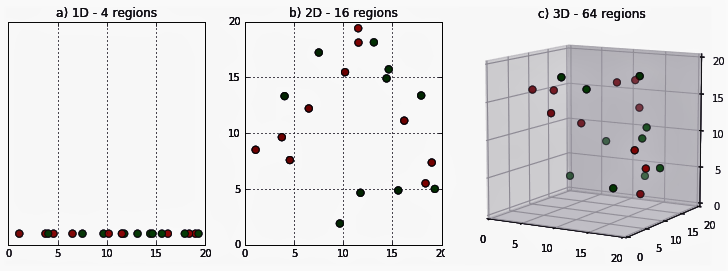
• if the number predictors becomes to large, we have have to reduce them

https://medium.com/analytics-vidhya/the-curse-of-dimensionality-and-its-cure-f9891ab72e5c

Solutions

• features selection (we did this before)
• dimensionality reduction (we will cover this later)

https://neptune.ai/blog/dimensionality-reduction

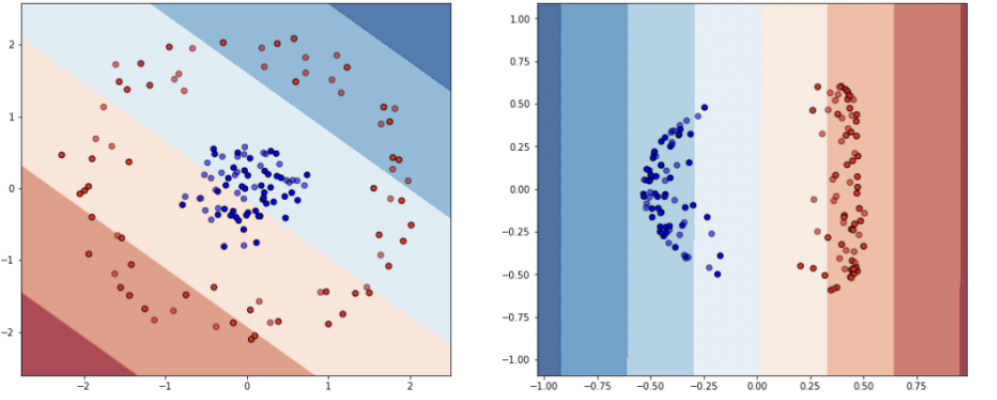
Problem 2: Differing Scales of Predictors

• If we just calculate the distance, the influence of weight is much lower!

Solution: Scaling of Predictors

• We have no parameter in the model (compare in linear models) that adjust for the scale of
• In such cases we can prepare the data before training the model
  • Normalization of a Variable is putting everything between and .

  • Standardization of a Variable is removing the mean and dividing by the deviation.

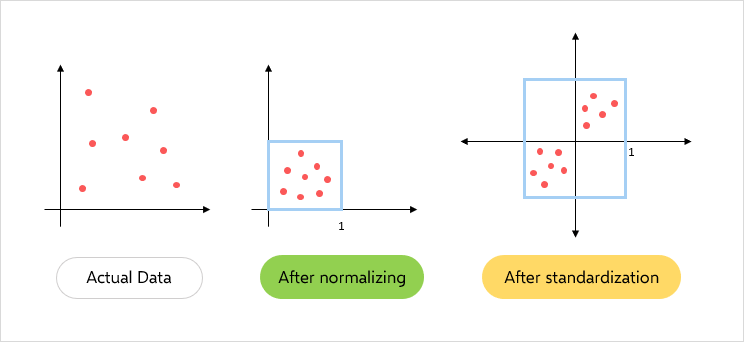
• Normalization bounds the values between 0 and 1 based on the min and max values
• Standardization does not bound values to a specific range if we have outliers

https://becominghuman.ai/what-does-feature-scaling-mean-when-to-normalize-data-and-when-to-standardize-data-c3de654405ed

Task

• perform a normalization of the Beak length and a standardization of the Weight.

10 minutes, Solution

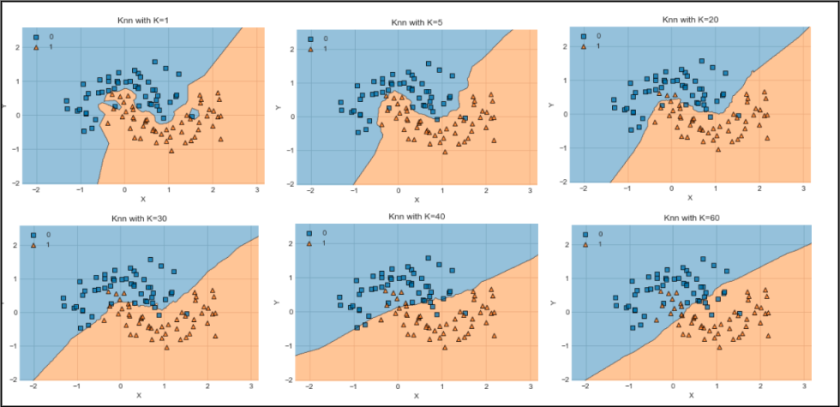
Problem 3: How many neighbors to consider?

https://i0.wp.com/neptune.ai/wp-content/uploads/KNN-diagram.png?resize=840%2C407&ssl=1

• best choice of k depends upon the data
  • larger values of reduces effect of the noise, but make decision boundaries between classes less distinct
  • smaller values of make decision boundaries more jagged and less distinct (over-fitting)
• usually found by
  • grid search: trying out different during cross-validation

• What is a good estimate of the beak depth of number 6?

Observation		Species	Beak length in mm	Beak depth in mm g
1	1	Gentoo	40	19	?
2	1	Gentoo	39	21	?
3	1	Gentoo	42	23	?
4	0	Adélie	20	18	?
5	0	Adélie	25	17	?
6	0	Adélie	26		?

• (2)-nearest neighbors based on a single feature Class

Case Study

• We will classify the penguin species and sex based on their characteristics using NN, grid search and data preprocessing.

https://www.scoopnest.com/user/AFP/1035147372572102656-do-you-know-your-gentoo-from-your-adelie-penguins-infographic-on-10-of-the-world39s-species-after

7 Classification and Advanced Supervised Learning

45 min